Next: 8章の演習問題 Up: 種々の断面形状を有する棒のねじり問題 Previous: 長方形断面棒のねじり Contents Index
図に示す中空断面棒のように ,断面が2つ以上の閉曲線
![]() ,
,![]() ,
,![]() ,
,![]() で囲まれている複連結領域の場合は ,
式(8.21)において閉曲線の数だけの定数 ,
で囲まれている複連結領域の場合は ,
式(8.21)において閉曲線の数だけの定数 ,
![]() が必要である.
ここで ,その内の一つは
が必要である.
ここで ,その内の一つは![]() に含めることができるから ,
例えば ,外側の境界上の定数を零(
に含めることができるから ,
例えば ,外側の境界上の定数を零(![]() とすることができる.
例として ,一つの穴を持つ中空断面棒について考えよう.
この場合の境界条件は
とすることができる.
例として ,一つの穴を持つ中空断面棒について考えよう.
この場合の境界条件は
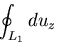 |
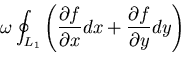 |
||
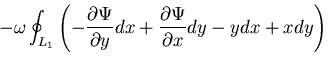 |
|||
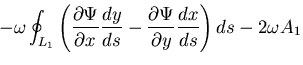 |
|||
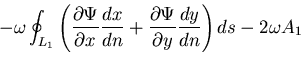 |
|||
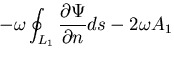 |
(535) |
Akihiro Nakatani 2001-06-25