長方形断面棒のねじり

Figure 8.2: 長方形断面

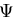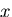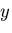図に示す長方形断面棒のねじり問題について考えよう． は ，の偶関数であるから 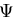，を 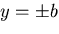で零になるように次式のようにおく．

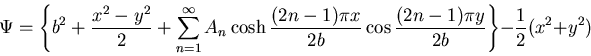$$\Psi = \left\{b^2 + \frac{x^2 - y^2}{2} + \sum_{n=1}^\infty ... ...cos \frac{(2n - 1)\pi y}{2b} \right\} - \frac{1}{2}(x^2 + y^2)$$ (529)

ここで ，上式のかっこ{ }内は調和関数であるから ， 上式で表される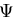は基礎方程式(8.27)を満足する． ただし 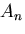，は未知定数であり 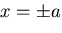，の境界条件:

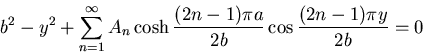$$b^2 - y^2 + \sum_{n=1}^{\infty}A_n \cosh \frac{(2n - 1)\pi a}{2b} \cos \frac{(2n-1)\pi y}{2b} =0$$ (530)

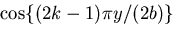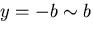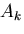より決定される． フーリエ級数の直交性を利用して ， を上式の両辺に乗じての 範囲で積分すれば ，未知係数は次のように求まり 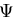， は決定される．

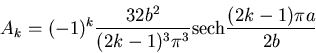$$A_k = (-1)^k \frac{32b^2}{(2k-1)^3\pi^3} \mbox{sech} \frac{(2k-1)\pi a}{2b}$$ (531)

応力成分およびねじりモーメントは ，式(8.25)と式 (8.28)とにより ，

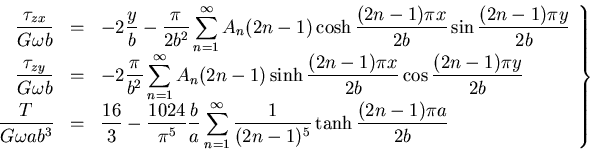$$\left. \begin{array}{rcl} \displaystyle\frac{\tau_{zx}}{G\om... ...(2n - 1)^5} \tanh \frac{(2n - 1)\pi a}{2b} \end{array}\right\}$$ (532)