Next: 熱応力問題 Up: ねじり問題 Previous: 中空断面棒のねじり Contents Index
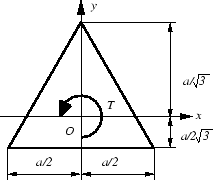
図に示すように一辺の長さが![]() の正三角形の断面を有する棒が,
ねじりモーメント
の正三角形の断面を有する棒が,
ねじりモーメント![]() を受けている場合について,以下の問に答えなさい.
ただし,棒のせん断弾性係数を
を受けている場合について,以下の問に答えなさい.
ただし,棒のせん断弾性係数を ![]() とする.
とする.
(1) ねじりの応力関数 ![]() を,
を,
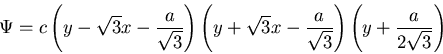 |
(538) |
(2) 単位長さあたりのねじれ角 ![]() を,
を,![]() で表しなさい.
で表しなさい.
(3) 応力成分,
![]() ,
,
![]() を,求めなさい.
また,
を,求めなさい.
また,![]() ,
,![]() 軸を含む面内(
軸を含む面内(![]() のせん断応力分布が
のせん断応力分布が![]() の値によっ
てどのように変化するかを図で示しなさい.
の値によっ
てどのように変化するかを図で示しなさい.
(4) ゆがみ関数 ![]() を求めなさい.
さらに,ねじりを加える前に平面であった面の
を求めなさい.
さらに,ねじりを加える前に平面であった面の![]() 方向変位を示す等値線を
模式的に示しなさい.
方向変位を示す等値線を
模式的に示しなさい.
ねじりの応力関数 ![]() を,
を,
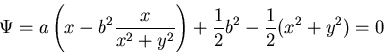 |
(539) |
(1) 応力関数は,ポアソン方程式を満足することを確認しなさい.
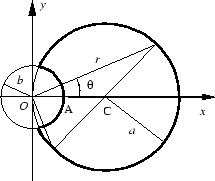
(2) また,![]() は,図に示すような,切欠きを有する円形断面の境
界で,
は,図に示すような,切欠きを有する円形断面の境
界で,![]() を満足することを示しなさい.
(ヒント
を満足することを示しなさい.
(ヒント
![]() などを用いて,
などを用いて,![]() に変換する.)
に変換する.)