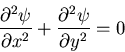前節の[III]の問題を考える.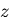 軸まわりのねじりモーメント
軸まわりのねじりモーメント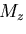 を慣
例にならって"トルク"の頭文字
を慣
例にならって"トルク"の頭文字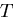 と表すことにする.ねじりが加えられて
いる両端から十分に離れた棒の中央部では,応力状態は,どの断面をとって見
ても同一となる.したがって,この問題は一つの断面のみを考えればよいから
2次元境界値問題として扱える.サンブナンのねじり問題
(St. Venant's torsion problem)という.
と表すことにする.ねじりが加えられて
いる両端から十分に離れた棒の中央部では,応力状態は,どの断面をとって見
ても同一となる.したがって,この問題は一つの断面のみを考えればよいから
2次元境界値問題として扱える.サンブナンのねじり問題
(St. Venant's torsion problem)という.
棒の断面で変位が0の点(ねじりの中心)を原点にとる.軸方向の単位長さあた
りのねじれ角(比ねじれ角)を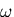 とすると,
とすると,
となる.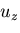 は,
は, 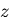 に無関係で,
に無関係で,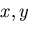 のみの関数であるというこ
とは,いえるから,未知関数
のみの関数であるというこ
とは,いえるから,未知関数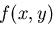 を導入して,
を導入して,
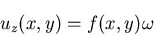 |
(501) |
すなわち,棒がねじりをうけると平面であった断面が,この関数の形に面外方
向に変形することになる.このような湾曲をゆがみ
(warping)と呼び,
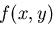 のことをゆがみ関数
(warping function)とよぶ.
のことをゆがみ関数
(warping function)とよぶ.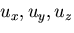 をひずみ変位関係に代入して,さらに,応力ひずみ関係に代入する
と,
をひずみ変位関係に代入して,さらに,応力ひずみ関係に代入する
と,
| |
|
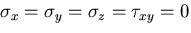 |
|
| |
|
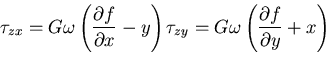 |
(502) |
を得る.
一方,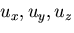 をナビアの方程式に代入すると,関数
をナビアの方程式に代入すると,関数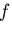 は,次の
微分方程式を満足する平面調和関数であることがわかる.
は,次の
微分方程式を満足する平面調和関数であることがわかる.
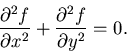 |
(503) |
次に,境界条件を考える.側面では,
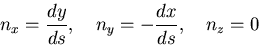 |
(504) |
であるから,
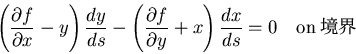 |
(505) |
したがって,関数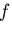 は,境界上で上式を満足する平面調和関数である.一
方,断面に作用するねじりモーメント
は,境界上で上式を満足する平面調和関数である.一
方,断面に作用するねじりモーメント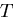 は,
は,
ここで,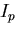 は,断面2次極モーメントであり,
は,断面2次極モーメントであり,
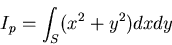 |
(507) |
である.したがって,ねじりモーメント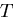 が与えられたならば,比ねじれ
角
が与えられたならば,比ねじれ
角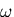 は,式(8.14)により決定される.もし,
は,式(8.14)により決定される.もし,
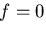 であるならば,
であるならば,
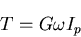 |
(508) |
となり,材料力学で学んだ中実,中空丸棒のねじり問題の解に一致する.
次に,関数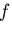 が満足しなければならない側面の境界条件式(8.13)を
書き直すと,
が満足しなければならない側面の境界条件式(8.13)を
書き直すと,
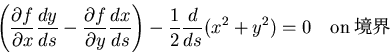 |
(509) |
さらに,以下のコーシー・リーマンの関係を満足する,平面調和関数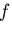 に
共役な平面調和関数
に
共役な平面調和関数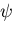 を導入する.
を導入する.
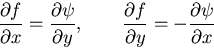 |
(510) |
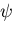 は,次の関係を満足する.
は,次の関係を満足する.
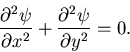 |
(511) |
境界条件式は,調和関数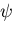 を用いて次のように書き直せる.
を用いて次のように書き直せる.
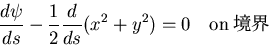 |
(512) |
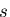 で積分すれば,
で積分すれば,
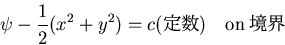 |
(513) |
ここで,断面が一つの閉曲線で囲まれている場合(単連結領域)は,定数を0と
おいてよい.
一方,応力成分は,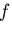 のかわりに,
のかわりに,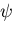 を用いると,
を用いると,
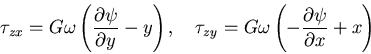 |
(514) |
である.いま,
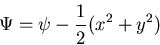 |
(515) |
なる関数 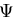 を導入すれば,
を導入すれば,
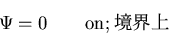 |
(516) |
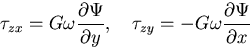 |
(517) |
となる.この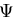 のことをねじり応力関数
(torsional stress
function)または,プラントル関数
(Prandtl function)という.
のことをねじり応力関数
(torsional stress
function)または,プラントル関数
(Prandtl function)という.
 に対する関係
に対する関係
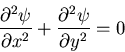 |
(518) |
から,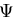 の満足すべきねじりの基礎方程式
の満足すべきねじりの基礎方程式
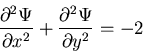 |
(519) |
を得る.また,ねじりモーメント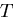 は,
は,
となる.結局,サンブナンのねじり問題はポアソン方程式を満足する応力関数
を境界上で0となるように決定する問題に帰着される.
Akihiro Nakatani
2001-06-25
![]() 軸まわりのねじりモーメント
軸まわりのねじりモーメント![]() を慣
例にならって"トルク"の頭文字
を慣
例にならって"トルク"の頭文字![]() と表すことにする.ねじりが加えられて
いる両端から十分に離れた棒の中央部では,応力状態は,どの断面をとって見
ても同一となる.したがって,この問題は一つの断面のみを考えればよいから
2次元境界値問題として扱える.サンブナンのねじり問題
(St. Venant's torsion problem)という.
と表すことにする.ねじりが加えられて
いる両端から十分に離れた棒の中央部では,応力状態は,どの断面をとって見
ても同一となる.したがって,この問題は一つの断面のみを考えればよいから
2次元境界値問題として扱える.サンブナンのねじり問題
(St. Venant's torsion problem)という.
![]() とすると,
とすると,
![]() をナビアの方程式に代入すると,関数
をナビアの方程式に代入すると,関数![]() は,次の
微分方程式を満足する平面調和関数であることがわかる.
は,次の
微分方程式を満足する平面調和関数であることがわかる.
![]() が満足しなければならない側面の境界条件式(8.13)を
書き直すと,
が満足しなければならない側面の境界条件式(8.13)を
書き直すと,
![]() のかわりに,
のかわりに,![]() を用いると,
を用いると,