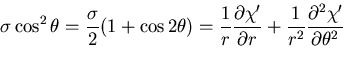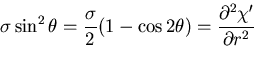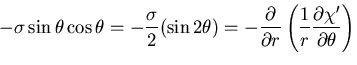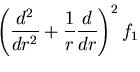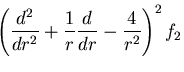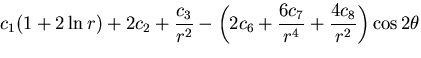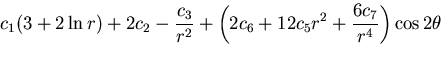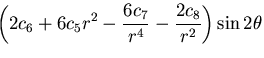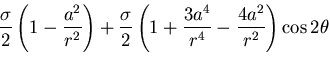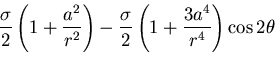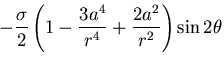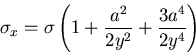次に,2次元の極座標系における応力関数と重調和方程式を求めることにする.
(1)極座標系のつりあい方程式とひずみの適合条件よりこれらをともに満足するような
応力関数の基礎式と応力成分を直接導く方法と,(2)座標変換を用いて基礎式と
応力の表示式を極座標系に書き改める方法とが考えられる.
ここでは,(2)の方法による.
極座標系の応力成分は,
と書ける.
また,直角座標系の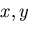 に関する偏導関数は,
に関する偏導関数は,
となるので,結局
物体力を0であるとすると,
となる.
一方,
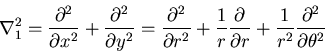 |
(433) |
となるから,
応力関数の満足すべき方程式は,
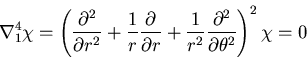 |
(434) |
となる.
この重調和方程式の一般解は,
で与えられる.
とくに,軸対称問題(axisymmetric problem)
では,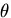 に関する偏導関数は,0であるので,応力は,
に関する偏導関数は,0であるので,応力は,
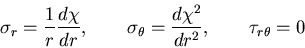 |
(436) |
となり,重調和方程式は,
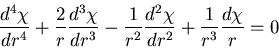 |
(437) |
となり,これは,同次方程式であるから,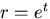 のような変数
のような変数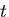 を導入すると,
を導入すると,
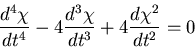 |
(438) |
のような定数係数の線形微分方程式となり,一般解は,
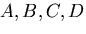 を積分定数として,
を積分定数として,
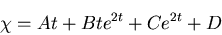 |
(439) |
となるので,結局,
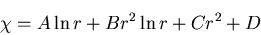 |
(440) |
これを用いると,応力は,
となることがわかる.
以下に極座標系におけるエアリーの応力関数の例を示す.
Figure 7.3:
極座標系における応力関数の適用例
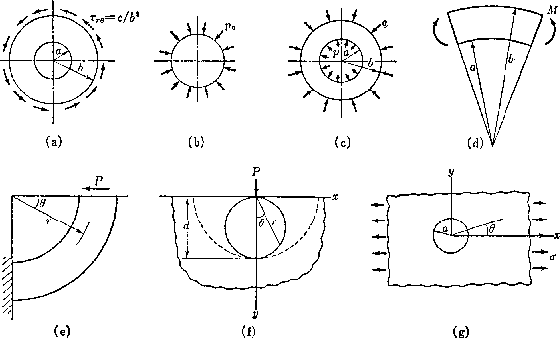 |
[I]
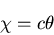 |
(442) |
この応力関数を式(7.58)に代入すると,
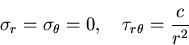 |
(443) |
となり,これは,例えば,図6.3(a)のように,
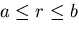 なる円環にせん断応力
なる円環にせん断応力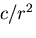 がはたらく場合となる.外周
(
がはたらく場合となる.外周
(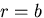 で,
で,
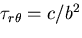 が作用すると,
が作用すると,
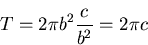 |
(444) |
なるねじりモーメントが作用する.したがって,
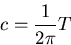 |
(445) |
となる.そして,円環が内周(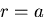 )で固定されていると,
円周に沿って一様なせん断応力
)で固定されていると,
円周に沿って一様なせん断応力
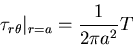 |
(446) |
を生じる.
[II]
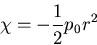 |
(447) |
このとき,式(7.58)から
 |
(448) |
となり,図6.3(b)に示すような一様な外圧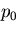 を受ける中実円柱を表すことになる.
を受ける中実円柱を表すことになる.
[III] 図6.3(c)のような,一様な内外圧をうける円筒
内外圧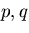 を受ける円筒を考える.
このとき軸対称だから,応力関数は式(7.66)である.
境界条件は,
を受ける円筒を考える.
このとき軸対称だから,応力関数は式(7.66)である.
境界条件は,
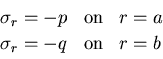 |
(449) |
であるから,式(7.67) の定数のうち2個,例えば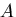 と
と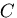 を
決めると境界条件は満たされる.
を
決めると境界条件は満たされる.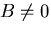 とするとき,式(7.67)を
応力ひずみ関係式に代入してひずみを求め,これを積分して接線方向の変位を求めると,
平面ひずみの場合,
とするとき,式(7.67)を
応力ひずみ関係式に代入してひずみを求め,これを積分して接線方向の変位を求めると,
平面ひずみの場合,
 を定数として,
を定数として,
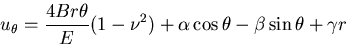 |
(450) |
となる.
ところで,第4項は,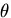 に無関係であり,第2, 3項も基準点から
に無関係であり,第2, 3項も基準点から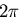 だけ
回ってもとの点に戻ったときには同じ値をとるが,
第1項は,
だけ
回ってもとの点に戻ったときには同じ値をとるが,
第1項は,
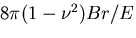 だけ変位が増加する.これは,変位が
多価であることを意味し,割れ目の無い円筒では物理的にありえない.
したがって,
だけ変位が増加する.これは,変位が
多価であることを意味し,割れ目の無い円筒では物理的にありえない.
したがって,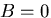 である.
よって,
である.
よって,
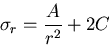 |
(451) |
を得るので,境界条件から定数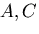 を決めると次の結果を得る.
を決めると次の結果を得る.
[IV]
厚さ1の曲りはりの曲げによる応力
図6.3(e)のような場合,境界条件は,
となるので,式(7.66)の定数は次のようになる.
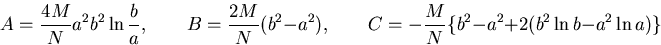 |
(454) |
ここで,
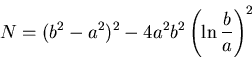 |
(455) |
である.よって応力分布は,
となる.
[V] 端面に働く力による曲りはりの曲げ
図6.3(d)のように,円弧状の軸を持ち,半径方向に力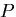 を受ける厚さ1のはりを考える.
を受ける厚さ1のはりを考える.
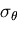 は,曲げモーメントに比例するから,
は,曲げモーメントに比例するから,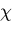 が
が
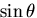 に比例するようにとればよいので,式(7.61)
で,
に比例するようにとればよいので,式(7.61)
で,
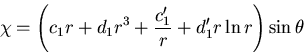 |
(457) |
とすればよい.よって,
| |
|
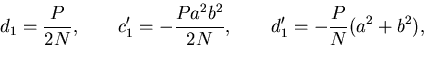 |
|
| |
|
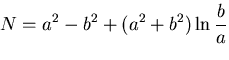 |
(458) |
となり,応力分布は
となる.
[VI] 直線縁に垂直な集中力を受ける半無限板
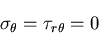 |
(460) |
であり,0でない応力成分は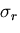 のみとする.
このような応力状態を単純半径応力分布
(simple radial stress distribution)
という.
単位厚さの半無限板が,集中荷重
のみとする.
このような応力状態を単純半径応力分布
(simple radial stress distribution)
という.
単位厚さの半無限板が,集中荷重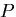 を受けるとし,
いま,図6.3(f)のように
を受けるとし,
いま,図6.3(f)のように 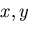 軸をとり,
軸をとり,
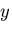 軸から反時計まわりに角度
軸から反時計まわりに角度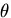 をとるとき,
単純半径応力分布であると仮定する.
応力のつりあい方程式から,
をとるとき,
単純半径応力分布であると仮定する.
応力のつりあい方程式から,
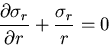 |
(461) |
また,
| |
|
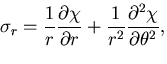 |
|
| |
|
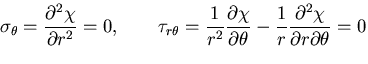 |
(462) |
さらに,重調和方程式は,式(7.88)の第2式,第3式を考慮すると
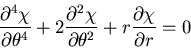 |
(463) |
のようになる.
これを解くために,
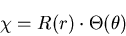 |
(464) |
のように変数分離を行なって,
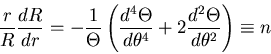 |
(465) |
とおくと,
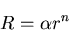 |
(466) |
を得る.さらに,式(7.88)の第1式から,
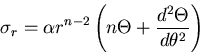 |
(467) |
となる.一方,式(7.87)から,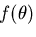 を
を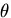 の
任意の関数とすると,
の
任意の関数とすると,
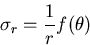 |
(468) |
とおくことができるから,
これらが等しいことから,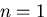 , すなわち,
, すなわち,
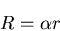 |
(469) |
を得る.また,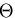 については,
については, を積分定数として,
を積分定数として,
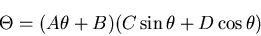 |
(470) |
となるので,
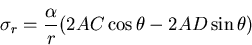 |
(471) |
ところで,
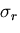 は,
は,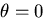 に対して対称であるから,
に対して対称であるから,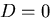 となり,
となり,
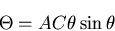 |
(472) |
すなわち,
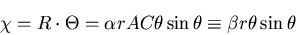 |
(473) |
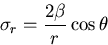 |
(474) |
を得る.
これから,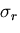 が一定の軌跡は境界に接する円となることがわかる.
さて,図の(f)のような破線の部分を考えると境界条件は,
が一定の軌跡は境界に接する円となることがわかる.
さて,図の(f)のような破線の部分を考えると境界条件は,
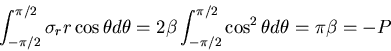 |
(475) |
のみとなりすべての境界条件を満足することがわかる.
これから,
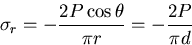 |
(476) |
を得る.
したがって,これを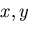 面の応力成分で表すと次のようになる.
面の応力成分で表すと次のようになる.
上の結果は,半無限板の縁に水平力を受ける場合に容易に拡張できる.
[VII] 円孔を持つ無限板の引張
図6.3(g)のように半径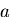 の円孔を持つ無限平板が十分遠方で
の円孔を持つ無限平板が十分遠方で
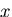 方向に一様な引張応力
方向に一様な引張応力
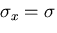 を受けるものとする.このとき境界条件は,
を受けるものとする.このとき境界条件は,
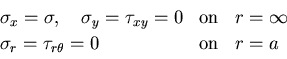 |
(478) |
となる.いま,円孔を持たない仮想的な場合を考え,応力が
のように応力関数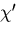 によって与えられるとする.
上式は,
によって与えられるとする.
上式は,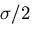 なる一定項と
なる一定項と
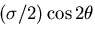 によって
によって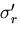 ,
,
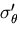 が表され,
が表され,
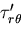 は
は
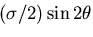 のみで表されることを考え,
円孔を持つ場合の応力関数として
のみで表されることを考え,
円孔を持つ場合の応力関数として
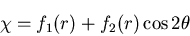 |
(480) |
の形をとるものとおく.これを式(7.60)に代入して,
を得る.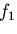 ,
,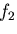 の一般解を求めて式(7.106)に代入すると,
次の結果が得られる.
の一般解を求めて式(7.106)に代入すると,
次の結果が得られる.
したがって,応力分布は
となる.ここで,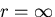 で応力が有限な値をとることから
で応力が有限な値をとることから
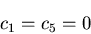 |
(484) |
であり,また,式(7.104)の境界条件を用いて
次の値が決められる.
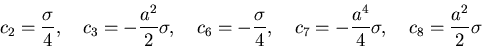 |
(485) |
したがって,応力分布は次式のようになる.
Figure 7.4:
円孔を持つ無限板の応力分布
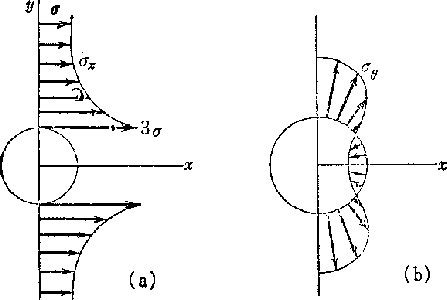 |
円孔まわりの応力集中を求めるために上式で とおき,
とおき,
 を
を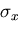 ,
,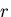 を
を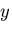 とおくと,
とおくと,
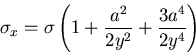 |
(487) |
となる.
この応力分布は図6.4(a)ようになり,
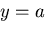 とおくことによって応力集中係数は3となることがわかる.
また,円孔周辺の
とおくことによって応力集中係数は3となることがわかる.
また,円孔周辺の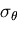 の値は図6.4(b)の様になる.
の値は図6.4(b)の様になる.
Akihiro Nakatani
2001-06-25
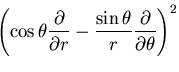
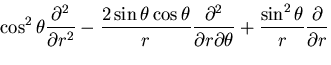
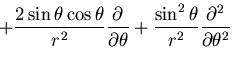
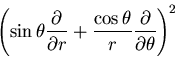
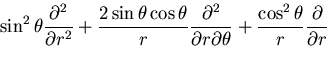
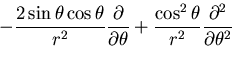
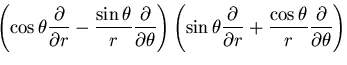
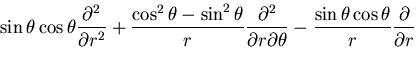
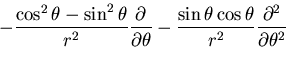
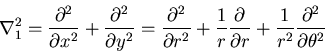
![]() に関する偏導関数は,0であるので,応力は,
に関する偏導関数は,0であるので,応力は,
![]() を受ける円筒を考える.
このとき軸対称だから,応力関数は式(7.66)である.
境界条件は,
を受ける円筒を考える.
このとき軸対称だから,応力関数は式(7.66)である.
境界条件は,
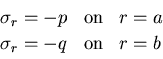
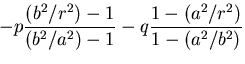
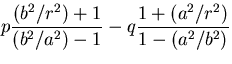
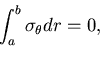
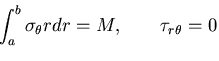
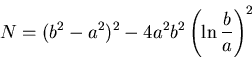
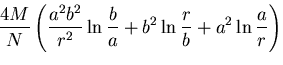
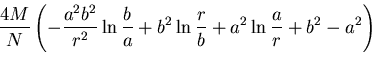
![]() を受ける厚さ1のはりを考える.
を受ける厚さ1のはりを考える.
![]() は,曲げモーメントに比例するから,
は,曲げモーメントに比例するから,![]() が
が
![]() に比例するようにとればよいので,式(7.61)
で,
に比例するようにとればよいので,式(7.61)
で,
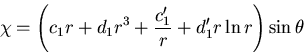
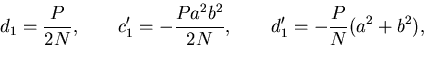
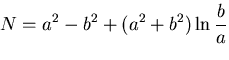
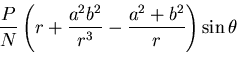
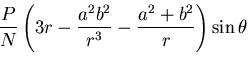
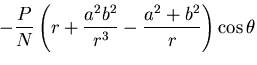
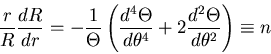
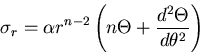
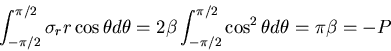
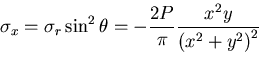
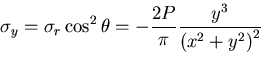
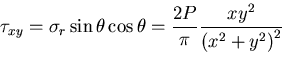
![]() の円孔を持つ無限平板が十分遠方で
の円孔を持つ無限平板が十分遠方で
![]() 方向に一様な引張応力
方向に一様な引張応力
![]() を受けるものとする.このとき境界条件は,
を受けるものとする.このとき境界条件は,