直角座標系における簡単なエアリーの応力関数

物体力が作用しないときの弾性体の平面問題は， 境界条件のもとで，重調和方程式を解けばよいことが 分かったが，一般にこの4階の微分方程式が解析的に解くことはできない． しかしながら，物体の形状や境界条件が単純な場合には応力関数を多項式で 表して解が求められる．いくつかの例を挙げることにする．

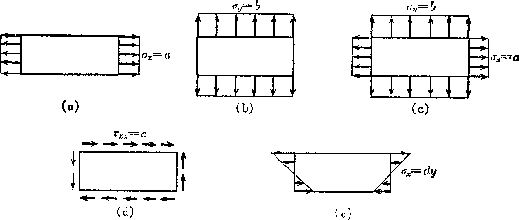
Figure 7.2: 直角座標系における応力関数の適用例

[I]

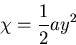$$\chi = \frac{1}{2}ay^2$$ (418)

のとき，応力分布は，

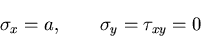$$\sigma_x=a, \qquad \sigma_y=\tau_{xy}=0$$ (419)

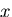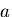となる．これは，方向になる応力を受ける平板に対応する．

[II]

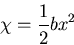$$\chi = \frac{1}{2}bx^2$$ (420)

のとき，応力分布は，

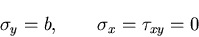$$\sigma_y=b, \qquad \sigma_x=\tau_{xy}=0$$ (421)

となる．これは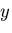，方向に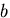なる応力を受ける平板に対応する．

[III]

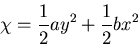$$\chi = \frac{1}{2}ay^2+\frac{1}{2}bx^2$$ (422)

のときは，[I], [II]の組合せに対応し，応力分布は，

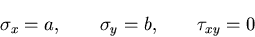$$\sigma_x=a, \qquad \sigma_y=b,\qquad \tau_{xy}=0$$ (423)

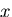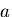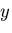となる． これは，方向に，方向に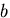なる2軸応力を受ける場合に対応する．

[IV]

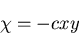$$\chi = -cxy$$ (424)

のとき，応力分布は，

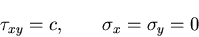$$\tau_{xy}=c, \qquad \sigma_x=\sigma_y=0$$ (425)

となる．これは，せん断応力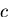の純粋せん断に対応する．

[V]

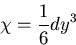$$\chi = \frac{1}{6}dy^3$$ (426)

のとき，応力分布は，

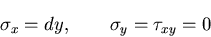$$\sigma_{x}=dy, \qquad \sigma_y=\tau_{xy}=0$$ (427)

これは，曲げをあらわす．

[VI]

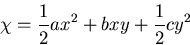$$\chi = \frac{1}{2}ax^2+bxy+\frac{1}{2}cy^2$$ (428)

のとき，応力分布は，

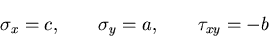$$\sigma_{x}=c, \qquad \sigma_y=a, \qquad \tau_{xy}=-b$$ (429)

であり，一様な2軸引張と純粋せん断を受ける場合となる．