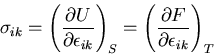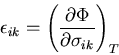ある変形を受けた物体について考える.
各物体点の変位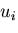 は,微小量
は,微小量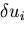 だけ変化する程度の
変形であると仮定する.
つりあい方程式から,内部応力
だけ変化する程度の
変形であると仮定する.
つりあい方程式から,内部応力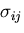 による仕事は,
力
による仕事は,
力
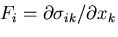 に
に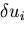 を掛けて,
それを物体の全体積にわたって積分して得られる.
を掛けて,
それを物体の全体積にわたって積分して得られる.
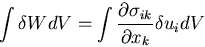 |
(210) |
ここで,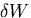 は,内部応力による単位体積あたりの仕事を示す.
発散定理を用いると,
は,内部応力による単位体積あたりの仕事を示す.
発散定理を用いると,
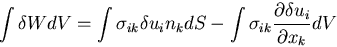 |
(211) |
無限遠方では変形を受けていない材料を考えて右辺第1項の積分表面を無限遠方に
近づけてみると,表面上では,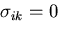 となり,第1項は消える.
となり,第1項は消える.
第2項は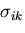 の対称性を考慮して,結局,
の対称性を考慮して,結局,
したがって,
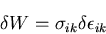 |
(213) |
この式は,ひずみテンソルの変化に応答する仕事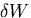 を定める.
を定める.
さて,エネルギ保存則(熱力学第一法則)から,
物体の単位体積あたりの内部エネルギの微小変化量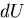 は,
単位体積あたりに物体が得る熱量
は,
単位体積あたりに物体が得る熱量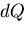 から,内部応力によりなされる
仕事を差し引いたものになる.
この熱量は可逆過程(すなわち,各時刻ごとに物体内の熱力学状態は平衡であるとする
場合)においては,
から,内部応力によりなされる
仕事を差し引いたものになる.
この熱量は可逆過程(すなわち,各時刻ごとに物体内の熱力学状態は平衡であるとする
場合)においては,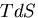 に等しい(ここで,Tは温度).したがって,
に等しい(ここで,Tは温度).したがって,
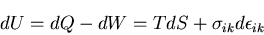 |
(214) |
[例]
ここで,周囲から一様な圧力を受ける場合の応力テンソルは,
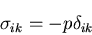 |
(215) |
このとき,
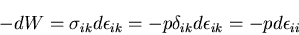 |
(216) |
ここで,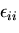 は体積変化の増分
は体積変化の増分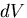 を表すので,
よく知られた,
を表すので,
よく知られた,
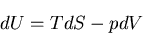 |
(217) |
が得られる.
さて,ヘルムホルツの自由エネルギ密度
(Helmholtz free energy density)
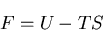 |
(218) |
を導入すると,
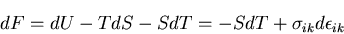 |
(219) |
と表せる.また,熱力学におけるギブスの自由エネルギ密度
(Gibbs free energy
density),
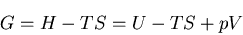 |
(220) |
を一般化した熱力学ポテンシャル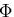 を導入する.
を導入する.
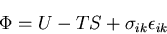 |
(221) |
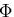 と
と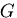 の違いは,
の違いは,
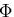 は,一様圧でない任意の応力に対する仕事に一般化されているだけでなく.
物体が一様圧を受ける時にも,
は,一様圧でない任意の応力に対する仕事に一般化されているだけでなく.
物体が一様圧を受ける時にも,
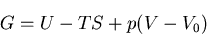 |
(222) |
となるので,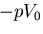 の分だけ異っていて,厳密には同じではない.さて,
式(5.15)から,式(5.13)を考慮すると,
の分だけ異っていて,厳密には同じではない.さて,
式(5.15)から,式(5.13)を考慮すると,
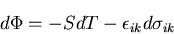 |
(223) |
を得る.
式(5.13)においては,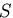 ,
,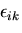 が,
式(5.17)においては,
が,
式(5.17)においては,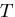 ,
,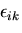 が,
独立な変数であり,応力テンソルの成分は,
が,
独立な変数であり,応力テンソルの成分は,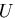 または,
または,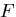 をそれぞれ,
エントロピ密度
(entropy density)
をそれぞれ,
エントロピ密度
(entropy density)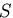 ,温度
,温度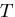 を
一定にした時のひずみテンソルの微分によって
導かれる.すなわち,
を
一定にした時のひずみテンソルの微分によって
導かれる.すなわち,
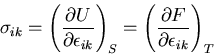 |
(224) |
同様にして,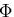 を応力成分
を応力成分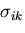 で微分すれば,
で微分すれば,
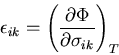 |
(225) |
を得る.
Akihiro Nakatani
2001-06-25
![]() は,微小量
は,微小量![]() だけ変化する程度の
変形であると仮定する.
つりあい方程式から,内部応力
だけ変化する程度の
変形であると仮定する.
つりあい方程式から,内部応力![]() による仕事は,
力
による仕事は,
力
![]() に
に![]() を掛けて,
それを物体の全体積にわたって積分して得られる.
を掛けて,
それを物体の全体積にわたって積分して得られる.
![]() の対称性を考慮して,結局,
の対称性を考慮して,結局,
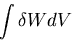
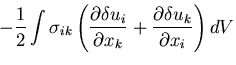
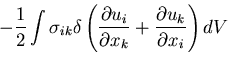
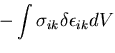
![]() は,
単位体積あたりに物体が得る熱量
は,
単位体積あたりに物体が得る熱量![]() から,内部応力によりなされる
仕事を差し引いたものになる.
この熱量は可逆過程(すなわち,各時刻ごとに物体内の熱力学状態は平衡であるとする
場合)においては,
から,内部応力によりなされる
仕事を差し引いたものになる.
この熱量は可逆過程(すなわち,各時刻ごとに物体内の熱力学状態は平衡であるとする
場合)においては,![]() に等しい(ここで,Tは温度).したがって,
に等しい(ここで,Tは温度).したがって,