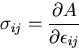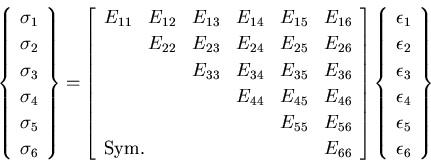前節で述べた熱力学的関係式は,
もとはといえばつりあい方程式から導いたものであり,
変形が微小であれば常に成立する関係である.
この関係式を具体的な境界値問題に適用するためには,
物体の内部エネルギ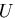 や自由エネルギ
や自由エネルギ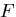 ,熱力学的ポテンシャル
,熱力学的ポテンシャル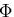 が具体的にどのようなものかを明らかにする必要がある.そして,
が具体的にどのようなものかを明らかにする必要がある.そして,
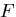 は,ひずみテンソル
は,ひずみテンソル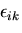 の関数,
の関数,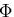 は,
応力テンソル
は,
応力テンソル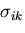 の関数で表現されていなければならない.
一般的にこれは,厳密には事実上不可能である.
しかしながら,ひずみが小さく,かつ温度変化
の関数で表現されていなければならない.
一般的にこれは,厳密には事実上不可能である.
しかしながら,ひずみが小さく,かつ温度変化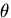 (
(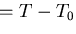 )
が小さい時には,自由エネルギをこれらのパラメータでべき級数に展開する
ことができる.
すなわち,
)
が小さい時には,自由エネルギをこれらのパラメータでべき級数に展開する
ことができる.
すなわち,
ここで,
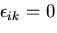 のとき,
のとき,
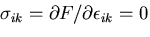 なので,ひずみの1次項は消える.
また,3次以上の高次項は無視できるものとすると,
なので,ひずみの1次項は消える.
また,3次以上の高次項は無視できるものとすると,
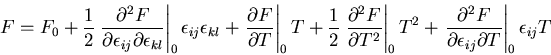 |
(227) |
ここで,
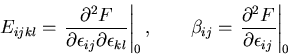 |
(228) |
とおくと,結局
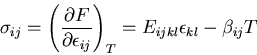 |
(229) |
を得る.
この式は,温度変化を伴う場合の
線形弾性体の構成式であり,
デュアメル・ノイマンの関係
(Duhamel-Neumann's relation)という.
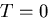 を考えると,温度変化が無視できる場合の
線形弾性体の構成式
を考えると,温度変化が無視できる場合の
線形弾性体の構成式
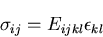 |
(230) |
を得る.
商法則により,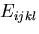 は4階のテンソルであり弾性係数テンソル
と呼ばれる.
は4階のテンソルであり弾性係数テンソル
と呼ばれる.
弾性係数テンソル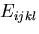 は,
は,
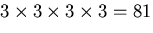 個の成分を有するが,
応力テンソル,ひずみテンソルの対称性
個の成分を有するが,
応力テンソル,ひずみテンソルの対称性
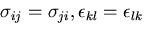 から
から
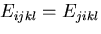 ,
,
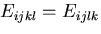 が成り立つので,
が成り立つので,
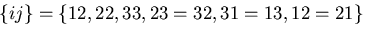 ,
,
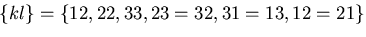 の
の
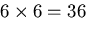 個の成分で表わされる.
個の成分で表わされる.
さらに,ひずみの二次形式で
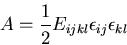 |
(231) |
の様に与えられるひずみエネルギ密度関数
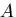 が存在し,応力が,
が存在し,応力が,
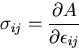 |
(232) |
与えられる場合には,
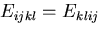 であるので,
であるので,
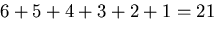 個の定数によって応力ひずみ関係が規定される.
応力テンソル,ひずみテンソルの指標を
個の定数によって応力ひずみ関係が規定される.
応力テンソル,ひずみテンソルの指標を
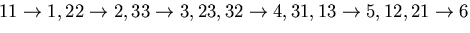 のようにフォークト記号
(Voigt notation)で表わす,すなわち,
のようにフォークト記号
(Voigt notation)で表わす,すなわち,
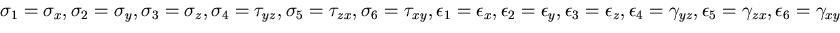 とおく.
また,弾性定数も
とおく.
また,弾性定数も
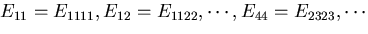 のようにおくと,
応力ひずみ関係は
のようにおくと,
応力ひずみ関係は
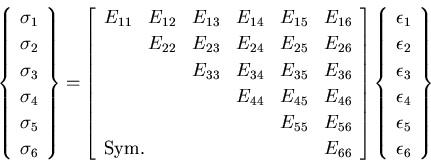 |
(233) |
の様に表わされる.このように最も異方性が強い場合でも
21個の弾性定数で表わされる.
Akihiro Nakatani
2001-06-25
![]() や自由エネルギ
や自由エネルギ![]() ,熱力学的ポテンシャル
,熱力学的ポテンシャル![]() が具体的にどのようなものかを明らかにする必要がある.そして,
が具体的にどのようなものかを明らかにする必要がある.そして,
![]() は,ひずみテンソル
は,ひずみテンソル![]() の関数,
の関数,![]() は,
応力テンソル
は,
応力テンソル![]() の関数で表現されていなければならない.
一般的にこれは,厳密には事実上不可能である.
しかしながら,ひずみが小さく,かつ温度変化
の関数で表現されていなければならない.
一般的にこれは,厳密には事実上不可能である.
しかしながら,ひずみが小さく,かつ温度変化![]() (
(![]() )
が小さい時には,自由エネルギをこれらのパラメータでべき級数に展開する
ことができる.
すなわち,
)
が小さい時には,自由エネルギをこれらのパラメータでべき級数に展開する
ことができる.
すなわち,
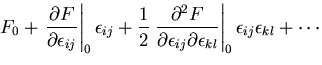
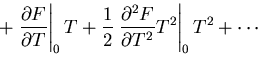
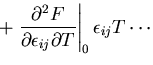
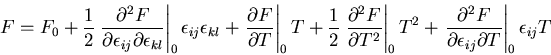
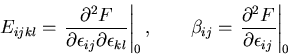
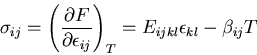
![]() は,
は,
![]() 個の成分を有するが,
応力テンソル,ひずみテンソルの対称性
個の成分を有するが,
応力テンソル,ひずみテンソルの対称性
![]() から
から
![]() ,
,
![]() が成り立つので,
が成り立つので,
![]() ,
,
![]() の
の
![]() 個の成分で表わされる.
個の成分で表わされる.