- ...
して振舞う
![[*]](file:/usr/share/latex2html/icons/footnote.gif)
- 一見固体として振舞うものの中にも長い年月
のスケールでみると流体として挙動するものもある.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
視的(ミクロスコピック)領域から,巨視的(マクロスコピック)領域
![[*]](file:/usr/share/latex2html/icons/footnote.gif)
- 例えば,地震の時に地質を伝わるP波とS波は,弾性論で
評価できる最も規模の大きいものであろう.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
し
![[*]](file:/usr/share/latex2html/icons/footnote.gif)
- たとえば,航空機の滑走用車輪は,強くしようとする
と重くなり,重くなればさらに強くしなければならないといった具
合にクリティカルな設計が要求されている.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
の位置の関数)の組を求める問題に帰着される
![[*]](file:/usr/share/latex2html/icons/footnote.gif)
- 密度
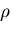 が変化するような場合は,さらに変数の数が増えるが,それ
らは,連続の式などといった別の保存則で補われる
が変化するような場合は,さらに変数の数が増えるが,それ
らは,連続の式などといった別の保存則で補われる
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(直交デカルト座標
![[*]](file:/usr/share/latex2html/icons/footnote.gif)
- そして,デカルト(de cartes)座標系のテンソ
ルはカーテシアンテンソル(cartesian tensor)と呼ばれる
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
となる
![[*]](file:/usr/share/latex2html/icons/footnote.gif)
- ここで,
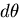 は,長さの次元を持たないの
で,
は,長さの次元を持たないの
で,
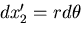 のように,
のように,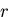 を乗じていることに注意する.つまり,
を乗じていることに注意する.つまり,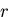 が大きくなれば,角度
が大きくなれば,角度
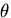 の微小変化は,
の微小変化は,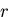 に比例して拡大される.
に比例して拡大される.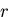 は形状因子
と呼ばれる.
は形状因子
と呼ばれる.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
となる
![[*]](file:/usr/share/latex2html/icons/footnote.gif)
- この場合も形状因子,
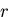 ,
, 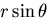 などが
必要であることに注意しよう.
などが
必要であることに注意しよう.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.