Figure 2.2:
座標変換
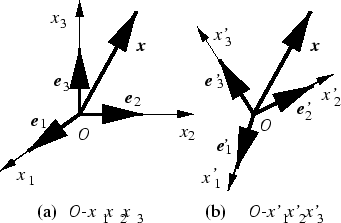 |
ある位置ベクトル
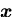 は,座標系
は,座標系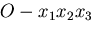 の成分
の成分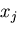 で表すと,
で表すと,
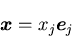 |
(26) |
別の座標系
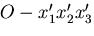 の成分
の成分
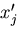 で表すと,
で表すと,
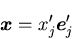 |
(27) |
となる.この二式を等しいとおいて,
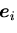 とのスカラー積
をとると
とのスカラー積
をとると
を得る.いま,
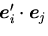 を,
を,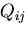 とおくことにすると,
とおくことにすると,
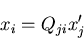 |
(31) |
と表される.同様にして,
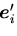 とのスカラー積をと
ると
とのスカラー積をと
ると
つまり,記号表示すると,
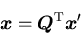 |
(36) |
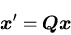 |
(37) |
これらから,
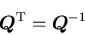 |
(38) |
であることがわかる.
次に,ベクトル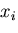 から微小量変化したベクトル
から微小量変化したベクトル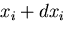 と,
ベクトル
と,
ベクトル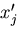 から微小量変化したベクトル
から微小量変化したベクトル
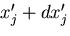 も,同じ関係によって変換されるから,
も,同じ関係によって変換されるから,
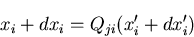 |
(39) |
展開して,
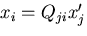 を代入すると,
を代入すると,
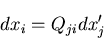 |
(40) |
同様にして,
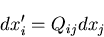 |
(41) |
が得られる.一般に,全微分 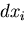 ,
, 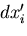 は,
は,
と表せるので,結局,
であることがわかる.
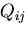 は,方向余弦(direction cosine)とよばれる.
は,方向余弦(direction cosine)とよばれる.
一般のベクトル
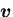 に対しても,
に対しても,
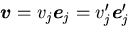 と表
せるから,同じ関係が成り立つ.
と表
せるから,同じ関係が成り立つ.
[例]
座標系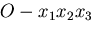 と,別の座標系
と,別の座標系
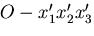 が与えられた時,
方向余弦
が与えられた時,
方向余弦 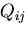 を成分とする行列
を成分とする行列
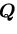 の行列式は,1で
あることを示そう.
の行列式は,1で
あることを示そう.
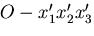 座標系の,
基底ベクトル,
座標系の,
基底ベクトル,
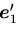 ,
,
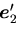 ,
,
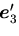 に平行な,
に平行な,
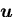 ,
,
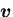 ,
,
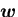 を考えると,これらは互いに直交する単位ベクトルであるから,
を考えると,これらは互いに直交する単位ベクトルであるから,
スカラー三重積を考えると,
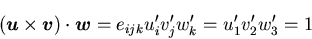 |
(46) |
となる.一方,
したがって,
![\begin{displaymath}
{\rm det}[\mbox{\boldmath$Q$}] = 1
\end{displaymath}](img139.gif) |
(51) |
であることが示された.
[例]
座標系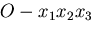 を
を
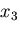 軸のまわりに,角度
軸のまわりに,角度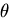 だけ回転した座標系
だけ回転した座標系
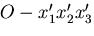 とを関係づける方向余弦
とを関係づける方向余弦
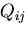 は,
は,
したがって,
![\begin{displaymath}[Q_{ij}]= \left[\begin{array}{ccc}
\cos\theta & \sin\theta & ...
...
-\sin\theta & \cos\theta & 0 \\
0 & 0 & 1
\end{array}\right]
\end{displaymath}](img146.gif) |
(55) |
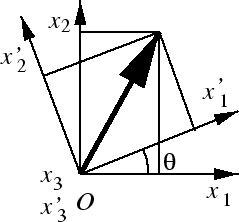
Figure 2.3:
 軸まわりの回転
軸まわりの回転
 |
[例]
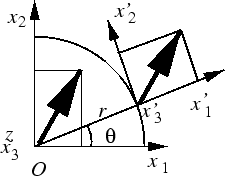
円柱(円筒)座標
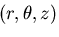 について直角座標系
について直角座標系
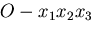 との関係を考えてみよう.
との関係を考えてみよう.
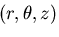 をその
まま,
をその
まま,
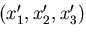 と考えると,これは,
線形変換にはならないので,いかに工夫しても,式(??)のような形
では表せないことがわかる.そこで,点P
と考えると,これは,
線形変換にはならないので,いかに工夫しても,式(??)のような形
では表せないことがわかる.そこで,点P
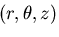 ,すな
わち,P
,すな
わち,P
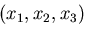 に,局所直角座標系
に,局所直角座標系
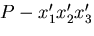 を考える.
を考える.
Figure 2.4:
円柱座標
 |
関係,
あるいは,その逆関係,
を用いて,
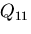 |
 |
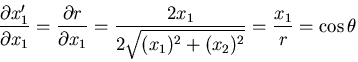 |
(62) |
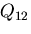 |
 |
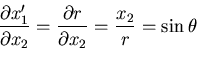 |
(63) |
 |
 |
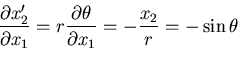 |
(64) |
 |
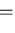 |
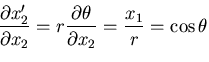 |
(65) |
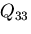 |
 |
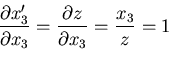 |
(66) |
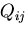 |
 |
 |
(67) |
したがって,
![\begin{displaymath}[Q_{ij}]= \left[\begin{array}{ccc}
\cos\theta & \sin\theta & ...
...
-\sin\theta & \cos\theta & 0 \\
0 & 0 & 1
\end{array}\right]
\end{displaymath}](img146.gif) |
(68) |
となる![[*]](file:/usr/share/latex2html/icons/footnote.gif) .
.
[例]
Figure 2.5:
球座標
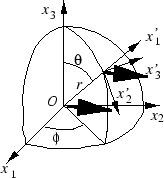 |
球座標
 についても,円柱座標と同様に,局所
直角座標系をとることによって,
についても,円柱座標と同様に,局所
直角座標系をとることによって,
および,
の関係を使って計算できる.詳細は演習として残すことにしてここ
では結果のみを示そう.
![\begin{displaymath}[Q_{ij}]= \left[\begin{array}{ccc}
\sin\theta\cos\phi & \sin\...
...\sin\theta \\
-\sin\phi & \cos\phi & 0 \\
\end{array}\right]
\end{displaymath}](img183.gif) |
(75) |
となる![[*]](file:/usr/share/latex2html/icons/footnote.gif) .
.
Akihiro Nakatani
2001-06-25
![]() は,座標系
は,座標系![]() の成分
の成分![]() で表すと,
で表すと,
![]() から微小量変化したベクトル
から微小量変化したベクトル![]() と,
ベクトル
と,
ベクトル![]() から微小量変化したベクトル
から微小量変化したベクトル
![]() も,同じ関係によって変換されるから,
も,同じ関係によって変換されるから,
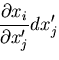
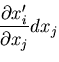
![]() は,方向余弦(direction cosine)とよばれる.
は,方向余弦(direction cosine)とよばれる.
![]() に対しても,
に対しても,
![]() と表
せるから,同じ関係が成り立つ.
と表
せるから,同じ関係が成り立つ.
![]() と,別の座標系
と,別の座標系
![]() が与えられた時,
方向余弦
が与えられた時,
方向余弦 ![]() を成分とする行列
を成分とする行列
![]() の行列式は,1で
あることを示そう.
の行列式は,1で
あることを示そう.
![]() 座標系の,
基底ベクトル,
座標系の,
基底ベクトル,
![]() ,
,
![]() ,
,
![]() に平行な,
に平行な,
![]() ,
,
![]() ,
,
![]() を考えると,これらは互いに直交する単位ベクトルであるから,
を考えると,これらは互いに直交する単位ベクトルであるから,
![]() を
を
![]() 軸のまわりに,角度
軸のまわりに,角度![]() だけ回転した座標系
だけ回転した座標系
![]() とを関係づける方向余弦
とを関係づける方向余弦
![]() は,
は,
![\begin{displaymath}[Q_{ij}]= \left[\begin{array}{ccc}
\cos\theta & \sin\theta & ...
...
-\sin\theta & \cos\theta & 0 \\
0 & 0 & 1
\end{array}\right]
\end{displaymath}](img146.gif)
![]() について直角座標系
について直角座標系
![]() との関係を考えてみよう.
との関係を考えてみよう.
![]() をその
まま,
をその
まま,
![]() と考えると,これは,
線形変換にはならないので,いかに工夫しても,式(??)のような形
では表せないことがわかる.そこで,点P
と考えると,これは,
線形変換にはならないので,いかに工夫しても,式(??)のような形
では表せないことがわかる.そこで,点P
![]() ,すな
わち,P
,すな
わち,P
![]() に,局所直角座標系
に,局所直角座標系
![]() を考える.
を考える.
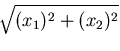
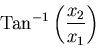
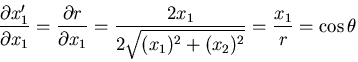
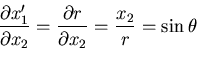
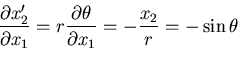
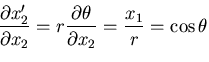
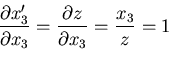
![\begin{displaymath}[Q_{ij}]= \left[\begin{array}{ccc}
\cos\theta & \sin\theta & ...
...
-\sin\theta & \cos\theta & 0 \\
0 & 0 & 1
\end{array}\right]
\end{displaymath}](img146.gif)
![]() についても,円柱座標と同様に,局所
直角座標系をとることによって,
についても,円柱座標と同様に,局所
直角座標系をとることによって,
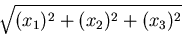
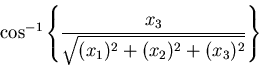
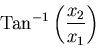
![\begin{displaymath}[Q_{ij}]= \left[\begin{array}{ccc}
\sin\theta\cos\phi & \sin\...
...\sin\theta \\
-\sin\phi & \cos\phi & 0 \\
\end{array}\right]
\end{displaymath}](img183.gif)