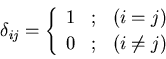二つのベクトル
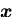 と
と
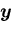 の内積(スカラー積)は,
の内積(スカラー積)は,
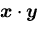 と表記され,両ベクトルのなす角
と表記され,両ベクトルのなす角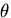 によって,
によって,
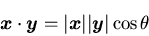 |
(10) |
で定義される.
基底ベクトルの内積,
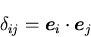 |
(11) |
で定義される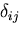 は,クロネッカーのデルタ(Kronecker's delta)
と呼ばれる.
とくに,直角座標
(直交デカルト座標
は,クロネッカーのデルタ(Kronecker's delta)
と呼ばれる.
とくに,直角座標
(直交デカルト座標![[*]](file:/usr/share/latex2html/icons/footnote.gif) の時,
の時,
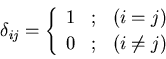 |
(12) |
『ポイント』
クロネッカーのデルタに関する以下の事項を確認して,無意識にこ
れらの性質が使えるように練習しておこう.
- 基底ベクトルの内積で定義される.
- その定義から,
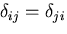 なる対称性がある.
なる対称性がある.
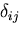 を行列の
を行列の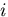 行
行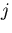 列の成分とすれば,その行列は,
単位行列である.
列の成分とすれば,その行列は,
単位行列である.
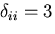 である.
である.
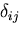 が含まれる項に,もし添字
が含まれる項に,もし添字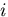 が現われた時,その添
字
が現われた時,その添
字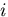 を
を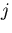 に置き換えて自ら消えてなくなるはたらきをする.同様
に,
に置き換えて自ら消えてなくなるはたらきをする.同様
に,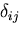 が含まれる項に,添字
が含まれる項に,添字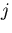 が現われた時,添字
が現われた時,添字
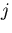 を
を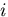 に置き換えて自ら消えてなくなるはたらきをする(指標の
置き換えの約束).
に置き換えて自ら消えてなくなるはたらきをする(指標の
置き換えの約束).
- 指標の置き換えの約束を使えば,
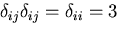 や,
や,
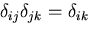 も容易に理解できるので,
覚えるまでもない.
も容易に理解できるので,
覚えるまでもない.
- また,クロネッカーデルタの性質を利用すると,
あるベクトル
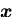 に,基底ベクトル
に,基底ベクトル
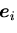 の内積
の内積
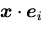 は,そのベクトルの成分
は,そのベクトルの成分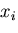 が取り出せ
る(ベクトル成分取り出しの内積).
が取り出せ
る(ベクトル成分取り出しの内積).
Akihiro Nakatani
2001-06-25
![]() と
と
![]() の内積(スカラー積)は,
の内積(スカラー積)は,
![]() と表記され,両ベクトルのなす角
と表記され,両ベクトルのなす角![]() によって,
によって,