楕円断面棒のねじり

Figure 8.1: 楕円断面棒

図に示す楕円断面棒のねじり問題について考えよう． 断面の境界形状を表す方程式は ，

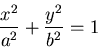$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$ (521)

であるから ，任意定数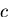を用いてねじりの応力関数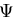を ，

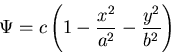$$\Psi = c\left(1 - \frac{x^2}{a^2} - \frac{y^2}{b^2}\right)$$ (522)

とおけば ，側面の境界条件式(8.24)は満足される． ここで ，任意定数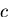は

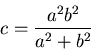$$c= \frac{a^2b^2}{a^2+b^2}$$ (523)

となる．したがって ，ねじりの応力関数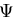は ，

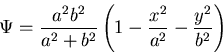$$\Psi = \frac{a^2b^2}{a^2+b^2}\left(1 - \frac{x^2}{a^2} - \frac{y^2}{b^2}\right)$$ (524)

上式を式(8.28)に代入すると ，ねじりモーメント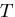は ，

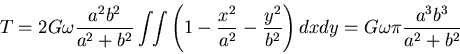$$T = 2G\omega\frac{a^2b^2}{a^2+b^2} \int\hspace*{-1mm}\int\le... ... \frac{y^2}{b^2}\right)dxdy = G\omega\pi\frac{a^3b^3}{a^2+b^2}$$ (525)

応力成分は式(8.25)より ，

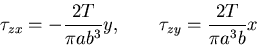$$\tau_{zx}=-\frac{2T}{\pi ab^3}y,\qquad \tau_{zy}= \frac{2T}{\pi a^3b}x$$ (526)

式(8.34)を式(8.10)に代入し積分すれば ，ゆがみ関数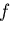は ，

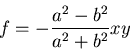$$f = - \frac{a^2 - b^2}{a^2 + b^2}xy$$ (527)

式(8.8)と式(8.9)とにより変位成分は

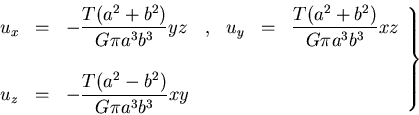$$\left. \begin{array}{lclclcl} u_x & = & -\displaystyle\frac{... ...\frac{T(a^2 - b^2)}{G\pi a^3b^3}xy & & & & \end{array}\right\}$$ (528)