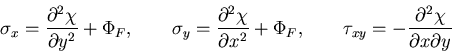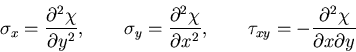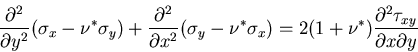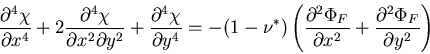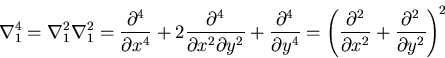物体力が保存力であるとき,ポテンシャル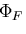 を用いて,
を用いて,
 |
(404) |
のようにあらわされる時,これらをつりあい方程式に代入すると,
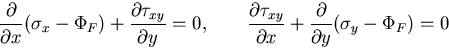 |
(405) |
ここで,天下り的に、
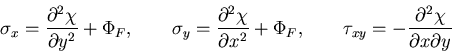 |
(406) |
とおけば,つりあい方程式は恒等的に満足される.
この関数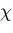 をエアリーの応力関数
(Airy's stress function)
という.特に,物体力が作用しない時には,
をエアリーの応力関数
(Airy's stress function)
という.特に,物体力が作用しない時には,
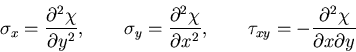 |
(407) |
となる.次に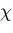 が満足すべき方程式について考える.すでに,
つりあい方程式は満足している(ように導入している)から,適合方
程式に代入すればよい.適合方程式に,応力ひずみ関係を代入して,
が満足すべき方程式について考える.すでに,
つりあい方程式は満足している(ように導入している)から,適合方
程式に代入すればよい.適合方程式に,応力ひずみ関係を代入して,
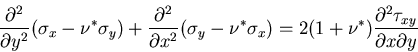 |
(408) |
を得る.この応力成分をエアリーの応力関数であらわすと,
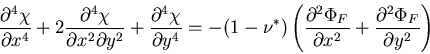 |
(409) |
あるいは,
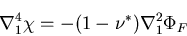 |
(410) |
を得る.
ここで,
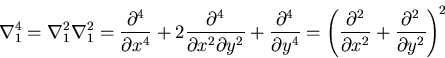 |
(411) |
とくに,物体力が作用しない時,
平面応力,平面ひずみ状態のいずれに対しても,
エアリーの応力関数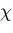 が満足すべき方程式は,
平面重調和方程式
が満足すべき方程式は,
平面重調和方程式
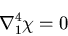 |
(412) |
となる.
Akihiro Nakatani
2001-06-25
![]() を用いて,
を用いて,