Next: エアリーの応力関数 Up: 平面問題 Previous: 平面応力 Contents Index
弾性力学の一般論を平面問題に適用する場合として, 平面ひずみ状態と,平面応力状態を考えてきた.これらの状態を 生じされる物理的な条件は大きく異なるがその基礎式は類似した 形式になり以下のように統一的に扱えることがわかる.
すなわち,
つりあい方程式は,
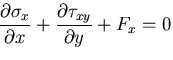 |
|||
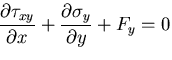 |
|||
| (396) |
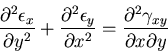 |
(397) |
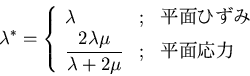 |
(398) |
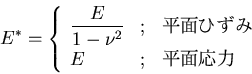 |
(399) |
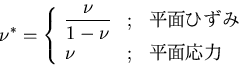 |
(400) |
| (401) |
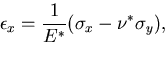 |
|||
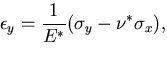 |
|||
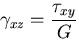 |
(402) |
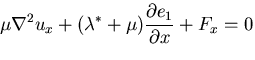 |
|||
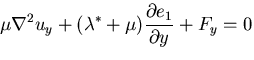 |
(403) |
Akihiro Nakatani 2001-06-25