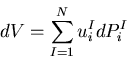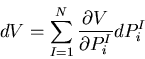これまでに述べてきたエネルギ原理では,境界での
力学的境界条件と幾何学的境界条件を
変化させずに領域内部の仮想変位や仮想応力を変化させた場合について考えてきた.
ここでは,つりあい状態にあるひずみエネルギやコンプリメンタリひずみ
エネルギが,境界条件の変化に対してどのように変わるかについて考える.
まず,力学的境界条件として与えられる
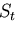 上の表面力は,
上の表面力は,
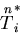 のまま固定して,
のまま固定して,
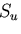 上の変位を
上の変位を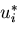 から,
から,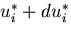 に変化させる.
このときのひずみエネルギの変化
に変化させる.
このときのひずみエネルギの変化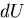 は,
は,
この式は,全ひずみエネルギの変化が,物体力および表面力のなす仕事
に等しいことを表しており,一般化したカスチリアノの第一定理
(generalized Castigliano's first theorem)といわれ,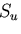 上の表面力
上の表面力
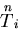 を決定するのに有益である.
今,
を決定するのに有益である.
今,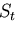 上の表面力と物体力が零であり,
上の表面力と物体力が零であり,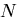 個の未知の集中力
個の未知の集中力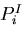 の作用点における集中力方向の変位
の作用点における集中力方向の変位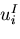 がわかっているとき(ここで,
がわかっているとき(ここで,
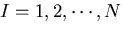 ),
),
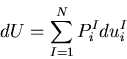 |
(358) |
となる.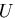 は,変位
は,変位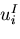 の関数であるから
の関数であるから
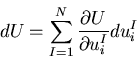 |
(359) |
と書ける.したがって,
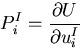 |
(360) |
が得られる.これは,
カスチリアノの第一定理
(Castigliano's first theorem),
または,エンゲッサーの定理
(Engesser's theorem)といわれ,
変位がわかっているときの集中力を求めるのに用いられる.
つぎに,幾何学的境界条件として与えられる
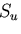 上の変位は,
上の変位は,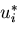 のまま固定して,
のまま固定して,
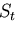 上の表面力を
上の表面力を
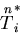 から,
から,
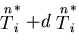 に変化させる.
物体力も
に変化させる.
物体力も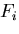 から
から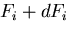 に変化するものとする.
このとき,
このときのコンプリメンタリひずみエネルギの変化
に変化するものとする.
このとき,
このときのコンプリメンタリひずみエネルギの変化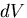 は,
は,
この式は,
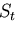 上の変位
上の変位
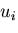 を求めるのに有益であり,
一般化したカスチリアノの第二定理
(generalized Castigliano's second theorem)といわれる.
を求めるのに有益であり,
一般化したカスチリアノの第二定理
(generalized Castigliano's second theorem)といわれる.
ここで,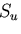 上で物体が固定され(
上で物体が固定され(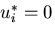 )でかつ,物体力が零であり,
)でかつ,物体力が零であり,
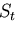 上の力がすべて集中力
上の力がすべて集中力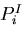 で与えられる場合には,
集中力の作用点の集中力方向の未知変位を
で与えられる場合には,
集中力の作用点の集中力方向の未知変位を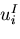 をとすると
(ここで,
をとすると
(ここで,
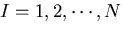 ),
),
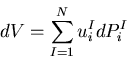 |
(361) |
となる.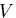 は,応力すなわち,表面力
は,応力すなわち,表面力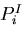 の関数であるから
の関数であるから
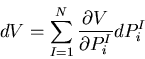 |
(362) |
と書ける.したがって,
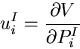 |
(363) |
が得られる.これを,
カスチリアノの第二定理
(Castigliano's second theorem),
または,単にカスチリアノの定理
(Castiglinano's theorem)といわれ,
集中荷重の作用点の変位を求めるのに便利である.
線形弾性体の場合には,ひずみエネルギ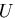 と
コンプリメンタリひずみエネルギ
と
コンプリメンタリひずみエネルギ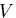 は,
等しいので,
は,
等しいので,
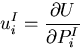 |
(364) |
と書ける.材料力学で学んだカスチリアノの定理は,この式である.
Akihiro Nakatani
2001-06-25
![]() 上の表面力は,
上の表面力は,
![]() のまま固定して,
のまま固定して,
![]() 上の変位を
上の変位を![]() から,
から,![]() に変化させる.
このときのひずみエネルギの変化
に変化させる.
このときのひずみエネルギの変化![]() は,
は,
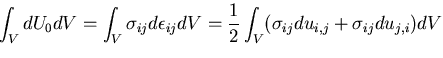
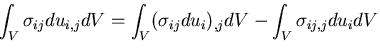
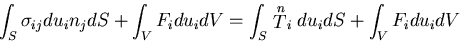
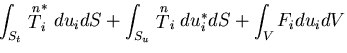
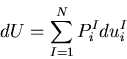
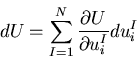
![]() 上の変位は,
上の変位は,![]() のまま固定して,
のまま固定して,
![]() 上の表面力を
上の表面力を
![]() から,
から,
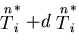 に変化させる.
物体力も
に変化させる.
物体力も![]() から
から![]() に変化するものとする.
このとき,
このときのコンプリメンタリひずみエネルギの変化
に変化するものとする.
このとき,
このときのコンプリメンタリひずみエネルギの変化![]() は,
は,
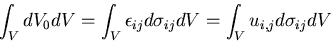
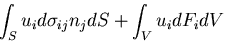
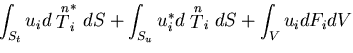
![]() 上で物体が固定され(
上で物体が固定され(![]() )でかつ,物体力が零であり,
)でかつ,物体力が零であり,
![]() 上の力がすべて集中力
上の力がすべて集中力![]() で与えられる場合には,
集中力の作用点の集中力方向の未知変位を
で与えられる場合には,
集中力の作用点の集中力方向の未知変位を![]() をとすると
(ここで,
をとすると
(ここで,
![]() ),
),