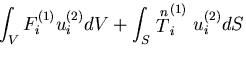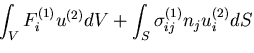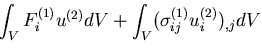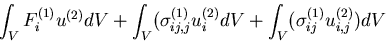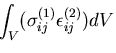物体力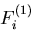 ,
,
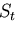 上で表面力
上で表面力
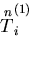 が与えられてつりあい状態(第1のつりあい状態とする)にある弾性体に生じる
応力を
が与えられてつりあい状態(第1のつりあい状態とする)にある弾性体に生じる
応力を
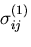 ,
変位を
,
変位を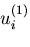 ,
ひずみを
,
ひずみを
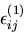 とする.
つぎに,物体力
とする.
つぎに,物体力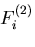 ,
,
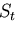 上で表面力
上で表面力
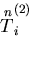 として与えられてつりあい状態(第2のつりあい状態とする)にある弾性体に生じる
応力を
として与えられてつりあい状態(第2のつりあい状態とする)にある弾性体に生じる
応力を
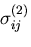 ,
変位を
,
変位を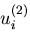 ,
ひずみを
,
ひずみを
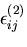 とする.
とする.
まず,第1の物体力の表面力が第2の変位になした仕事を考えると,
となる,同様に,第2の物体力の表面力が第1の変位になした仕事を考えると,
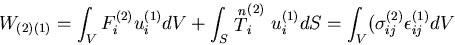 |
(354) |
となる.
これらの被積分項をフックの法則を用いて変形すれば,
となる.
したがって,
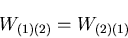 |
(356) |
または,
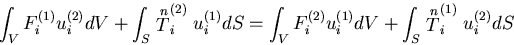 |
(357) |
これは,第1の外力が第2の変位に対してなす仕事は,
第2の外力が第1の変位に対してなす仕事に等しいことを表しており,
相反定理(reciprocal theorem)という.
材料力学で学ぶ
ベッティの相反定理
(Betti's reciprocal theorem),
は第1第2のつりあいが物体力が零で集中荷重を受ける
特別な場合で,
マクスウェルの相反定理
(Maxwell's reciprocal theorem)は,
さらに,その集中荷重の大きさが等しい
特別な場合である.
Akihiro Nakatani
2001-06-25
![]() ,
,
![]() 上で表面力
上で表面力
![]() が与えられてつりあい状態(第1のつりあい状態とする)にある弾性体に生じる
応力を
が与えられてつりあい状態(第1のつりあい状態とする)にある弾性体に生じる
応力を
![]() ,
変位を
,
変位を![]() ,
ひずみを
,
ひずみを
![]() とする.
つぎに,物体力
とする.
つぎに,物体力![]() ,
,
![]() 上で表面力
上で表面力
![]() として与えられてつりあい状態(第2のつりあい状態とする)にある弾性体に生じる
応力を
として与えられてつりあい状態(第2のつりあい状態とする)にある弾性体に生じる
応力を
![]() ,
変位を
,
変位を![]() ,
ひずみを
,
ひずみを
![]() とする.
とする.