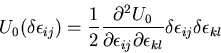内部仮想仕事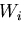 は,
仮想変位
は,
仮想変位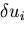 によるひずみエネルギの増加
によるひずみエネルギの増加 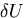 と考えられる.
と考えられる.
物体力や表面力が保存力
(conservative force)であり,
ポテンシャル 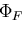 ,
,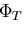 であるとすると,
であるとすると,
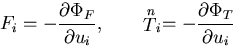 |
(332) |
のように表されるから,仮想仕事の原理は,
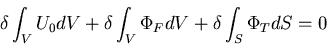 |
(333) |
すなわち,
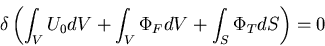 |
(334) |
ここで,
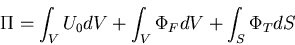 |
(335) |
を全ポテンシャルエネルギ
(total potential energy)という.
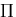 は,弾性体のひずみエネルギと物体力および表面力による
ポテンシャルエネルギを加えたものである.
微小な仮想変位
は,弾性体のひずみエネルギと物体力および表面力による
ポテンシャルエネルギを加えたものである.
微小な仮想変位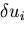 を与えても物体力と表面力が変化しないとすると,
を与えても物体力と表面力が変化しないとすると,
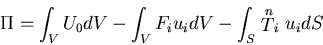 |
(336) |
と書ける.このように,
ポテンシャルエネルギは,位置エネルギともよばれ,外力のなす仕事は,
外力のポテンシャルエネルギの減少を表すので外力のなす仕事に負
の符号をつけたものである.
これを用いると,
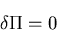 |
(337) |
となる.つまり,物体がつりあい状態にある時に,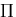 が停留値をとることを
意味している.
このことを,停留ポテンシャルエネルギの原理
(stationary principle of potential energy)という.
が停留値をとることを
意味している.
このことを,停留ポテンシャルエネルギの原理
(stationary principle of potential energy)という.
さて,この停留値が極小値であることを示そう.
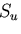 と
と 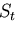 上の境界条件を満足する実変位
上の境界条件を満足する実変位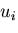 に対する
ポテンシャルエネルギ
に対する
ポテンシャルエネルギ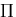 と
任意の仮想変位が加えられた場合の変位
と
任意の仮想変位が加えられた場合の変位
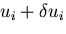 に対する
ポテンシャルエネルギ
に対する
ポテンシャルエネルギ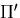 を比較してみる.
を比較してみる.
ここで,
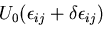 を
を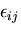 のまわりに Taylor 展開すると
のまわりに Taylor 展開すると
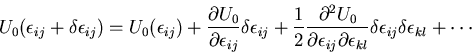 |
(339) |
高次の項を無視して,
となる.第1, 2, 3項の和は仮想仕事の原理式から0となる.
一方,
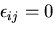 のとき,
のとき,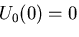 であり,
であり,
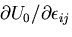 は,
は,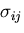 を意味するが,
応力ひずみ関係から応力も 0となり,
を意味するが,
応力ひずみ関係から応力も 0となり,
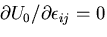 となる.したがって,
となる.したがって,
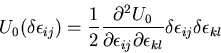 |
(341) |
となるので,
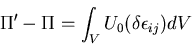 |
(342) |
となる.
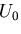 はひずみエネルギを表わす正値二次形式なので,
はひずみエネルギを表わす正値二次形式なので,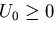 である.よって,
である.よって,
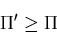 |
(343) |
となる.
このことから,無ひずみ状態(これを自然状態
(natural state)という)
の近傍では,ポテンシャルエネルギは極小値をもつことがわかる.
後で述べるように,弾性問題では解は唯一であるという原理から,
ポテンシャルエネルギの極小値は最小値であることになる.
したがって,ポテンシャルエネルギの停留を示す式は
最小値を意味している.
これを最小ポテンシャルエネルギの原理
(principle of minimum potential energy)という.
Akihiro Nakatani
2001-06-25
![]() は,
仮想変位
は,
仮想変位![]() によるひずみエネルギの増加
によるひずみエネルギの増加 ![]() と考えられる.
と考えられる.
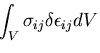
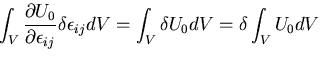
![]() と
と ![]() 上の境界条件を満足する実変位
上の境界条件を満足する実変位![]() に対する
ポテンシャルエネルギ
に対する
ポテンシャルエネルギ![]() と
任意の仮想変位が加えられた場合の変位
と
任意の仮想変位が加えられた場合の変位
![]() に対する
ポテンシャルエネルギ
に対する
ポテンシャルエネルギ![]() を比較してみる.
を比較してみる.
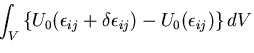
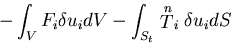
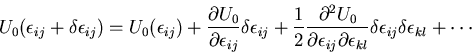
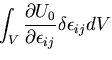
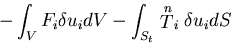
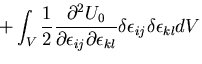
![]() のとき,
のとき,![]() であり,
であり,
![]() は,
は,![]() を意味するが,
応力ひずみ関係から応力も 0となり,
を意味するが,
応力ひずみ関係から応力も 0となり,
![]() となる.したがって,
となる.したがって,