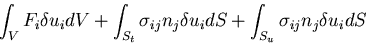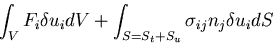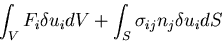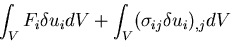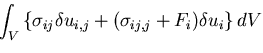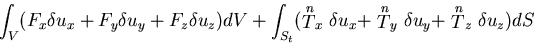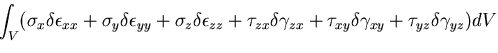物体力と表面力を受けてつりあい状態にある物体を考えよう.
物体は,体積(内部)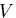 を持ち,境界(表面)
を持ち,境界(表面)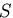 で囲まれているものとする.
このとき,境界
で囲まれているものとする.
このとき,境界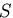 は,
は,
 |
(317) |
の2種類の境界に分けることができる.
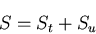 |
(318) |
ただし,面に垂直な方向は拘束されているが面の接線方向は自由に運動できる
といった具合に,方向を考慮することができるものとする.
さて,外力が作用するもとで静力学的につりあい状態にある弾性体に
おいて,物体内部の応力や変位の分布は唯一に決まり,その応力や
変位は,応力のつりあい方程式,ひずみの適合条件式(ひずみ変位関係),
を満足し,境界上で力学的,幾何学的境界条件を満足している.
このような実際に生じている変位を実変位といい,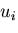 とする.
これに対して,
とする.
これに対して,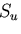 上の変位に関する境界条件,すなわち幾何学的な境界条件は
満足するが,
上の変位に関する境界条件,すなわち幾何学的な境界条件は
満足するが,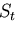 上の応力に関する境界条件,すなわち,力学的な
境界条件は必ずしも満足しないような仮想変位
(virtual displacement)を
上の応力に関する境界条件,すなわち,力学的な
境界条件は必ずしも満足しないような仮想変位
(virtual displacement)を
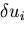 とあらわすことにする.
このような変位のことを幾何学的に許容な変位
(kinematically admissibledisplacement)という.
とあらわすことにする.
このような変位のことを幾何学的に許容な変位
(kinematically admissibledisplacement)という.
さて,物体には,体積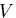 に対して物体力
に対して物体力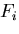 が,
境界
が,
境界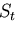 では,表面力
では,表面力
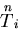 が作用する.
これらの力が仮想変位
が作用する.
これらの力が仮想変位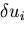 に対してなす仕事,すなわち
外部仮想仕事
(external virtual work)
に対してなす仕事,すなわち
外部仮想仕事
(external virtual work) 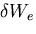 は,
は,
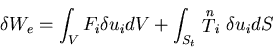 |
(319) |
となる.表面 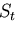 上で,コーシーの関係
上で,コーシーの関係
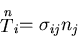 |
(320) |
が成り立つから,
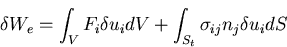 |
(321) |
さらに,仮想変位の定義から,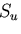 上で
上で
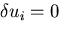 なので,
なので,
の様に書いても良い.
ここで,ガウス(Gauss)の発散定理(Gauss's divergence theorem)
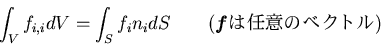 |
(323) |
を用いて,表面積分を体積積分に直すと,
となる.ここで,物体はつりあい状態にあるので,
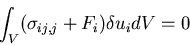 |
(325) |
また,応力成分が対称であることを用いれば,
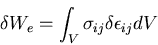 |
(326) |
を得る.ここで,
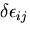 は,ひずみ変位関係
は,ひずみ変位関係
![\begin{displaymath}
\delta \epsilon_{ij}=
\delta\left[\frac12(u_{j,i}+ u_{i,j})\right]=
\frac12(\delta u_{j,i}+\delta u_{i,j})
\end{displaymath}](img788.gif) |
(327) |
によって仮想変位 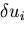 に対応する
仮想ひずみ(virtual strain)である.
これは,物体内部の力学的に許容な応力
に対応する
仮想ひずみ(virtual strain)である.
これは,物体内部の力学的に許容な応力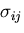 が,仮想ひずみ
が,仮想ひずみ
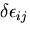 に対してなす内部仮想仕事
(internal virtual work)
に対してなす内部仮想仕事
(internal virtual work) 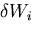 に対応することを意味している.
すなわち,
に対応することを意味している.
すなわち,
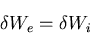 |
(328) |
結局,
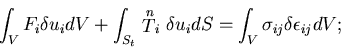 |
(329) |
これを仮想仕事の原理
(principle of virtual work)という.
この導出過程を逆にたどれば釣合方程式と力学的境界条件式が得られる.
したがって,仮想仕事の原理は,釣合方程式と力学的境界条件式と
等価である.
ここで,注意しなければならないのは,導出の過程で
応力ひずみ関係などの構成式を導入していないことである.
すなわち,仮想仕事の原理は,応力ひずみ関係に無関係に成立し,
弾性問題ばかりでなく塑性問題にも適用できる.
Akihiro Nakatani
2001-06-25
![]() を持ち,境界(表面)
を持ち,境界(表面)![]() で囲まれているものとする.
このとき,境界
で囲まれているものとする.
このとき,境界![]() は,
は,

![]() とする.
これに対して,
とする.
これに対して,![]() 上の変位に関する境界条件,すなわち幾何学的な境界条件は
満足するが,
上の変位に関する境界条件,すなわち幾何学的な境界条件は
満足するが,![]() 上の応力に関する境界条件,すなわち,力学的な
境界条件は必ずしも満足しないような仮想変位
(virtual displacement)を
上の応力に関する境界条件,すなわち,力学的な
境界条件は必ずしも満足しないような仮想変位
(virtual displacement)を
![]() とあらわすことにする.
このような変位のことを幾何学的に許容な変位
(kinematically admissibledisplacement)という.
とあらわすことにする.
このような変位のことを幾何学的に許容な変位
(kinematically admissibledisplacement)という.
![]() に対して物体力
に対して物体力![]() が,
境界
が,
境界![]() では,表面力
では,表面力
![]() が作用する.
これらの力が仮想変位
が作用する.
これらの力が仮想変位![]() に対してなす仕事,すなわち
外部仮想仕事
(external virtual work)
に対してなす仕事,すなわち
外部仮想仕事
(external virtual work) ![]() は,
は,