弾性体が外力を受けて変形する場合に,
外力は,物体に対して
仕事(work)をし,
熱力学第一法則(エネルギ保存則)により,
この仕事は,内部エネルギに変化する.
その一部は,熱となって物体の温度上昇に寄与するが,
残りはひずみエネルギ
(strain energy)となって
物体内部に蓄えられる.そして,
変形状態が緩やか(準静的
(quasi static))である場合には,
熱に変わるエネルギはごくわずかであり,物体の温度は変化しないで,
仕事はすべてひずみエネルギとなって物体の内部に蓄えられると考えてよい.
そして,外力を除くと物体はもとの形状にもどるので
ひずみエネルギは外部に放出される.
さて,図6.1のような微小六面体の応力状態,ひずみ状態を考える.
Figure 6.1:
微小六面体
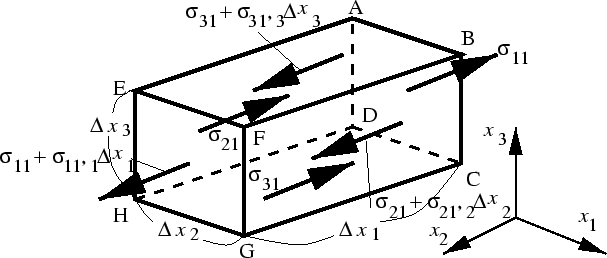 |
面ABCD の 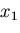 方向の変位を
方向の変位を 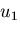 とすると,
とすると,
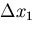 だけ離れた
面EFGHの変位は,
だけ離れた
面EFGHの変位は,
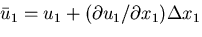 となる.また,面ABCDの垂直応力
となる.また,面ABCDの垂直応力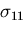 は,
面EFGHでは,
は,
面EFGHでは,
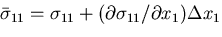 したがって応力0の状態から,これらの応力にいたるまでになす仕事を
考える.
変位が
したがって応力0の状態から,これらの応力にいたるまでになす仕事を
考える.
変位が は,時刻
は,時刻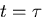 の時に,その値がわかっているものとし,
すなわち,
の時に,その値がわかっているものとし,
すなわち,
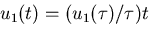 の様に
時間
の様に
時間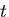 に比例して変化するものとすると,仕事は,
に比例して変化するものとすると,仕事は,
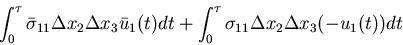 |
(279) |
と表される.時刻
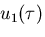 を単に,
を単に,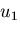 のように書くと,
のように書くと,
と表される.高次項を無視すると,
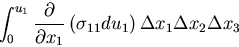 |
(281) |
同様にして,これらの面にはたらくせん断応力による仕事は,
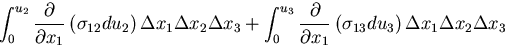 |
(282) |
であるから,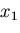 軸に垂直な面全体については,
これらの和をとって,
軸に垂直な面全体については,
これらの和をとって,
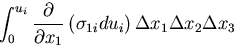 |
(283) |
で与えられる.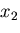 ,
,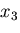 軸に垂直な面についても同様に考えると,
微小六面体全体についての応力のなす仕事
軸に垂直な面についても同様に考えると,
微小六面体全体についての応力のなす仕事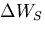 は次のようになる.
は次のようになる.
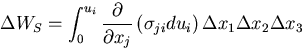 |
(284) |
一方,物体力
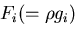 によりなされる仕事は,
六面体が微小であることを考慮して,
によりなされる仕事は,
六面体が微小であることを考慮して,
 方向については,
重心
方向については,
重心
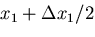 の点について,
変位
の点について,
変位
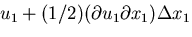 との積で表されると考えると,
との積で表されると考えると,
で与えられる.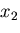 ,
,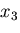 軸についても同様に考えると,
物体力による仕事
軸についても同様に考えると,
物体力による仕事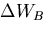 は,
は,
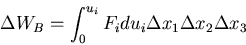 |
(286) |
となる.結局,微小六面体に蓄えられるひずみエネルギ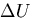 は,
は,
ここで,応力テンソルの対称性を考慮した.
つりあい方程式から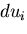 の項は消える.さらに,
ひずみ変位関係を適用すると,結局,
の項は消える.さらに,
ひずみ変位関係を適用すると,結局,
![\begin{displaymath}
\Delta U = \left[\int_0^{\epsilon_{ij}}%%
\sigma_{ij}d\epsilon_{ij}\right] \Delta x_1 \Delta x_2 \Delta x_3
\end{displaymath}](img720.gif) |
(288) |
を得る.
この関係は,一般に体積 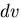 を持つ微小要素についても成り立つので,
単位体積当たりのひずみエネルギを
を持つ微小要素についても成り立つので,
単位体積当たりのひずみエネルギを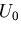 とすると,
とすると,
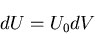 |
(289) |
となる.ここで,
である.この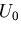 のことをひずみエネルギ密度関数
(strain energy
density function)という.
さて,ここで,線形弾性体の構成式を代入して積分し,
ひずみの無い状態
のことをひずみエネルギ密度関数
(strain energy
density function)という.
さて,ここで,線形弾性体の構成式を代入して積分し,
ひずみの無い状態
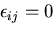 で,
で,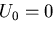 とすると,
とすると,
と表される.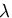 ,
,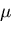 が正なので,
ひずみエネルギ密度関数は,負にならない.
すなわち,
が正なので,
ひずみエネルギ密度関数は,負にならない.
すなわち,
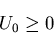 |
(294) |
さて,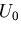 をひずみで微分し,応力ひずみ関係を用いると,
をひずみで微分し,応力ひずみ関係を用いると,
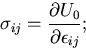 |
(295) |
| |
|
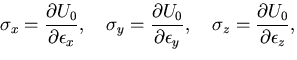 |
|
| |
|
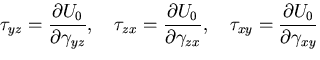 |
(296) |
が得られる.
これは,ヘルムホルツの自由エネルギ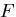 で温度やエントロピの変化を考えない場合の
式に当たる.
で温度やエントロピの変化を考えない場合の
式に当たる.
応力をひずみの関数であるとして,
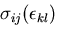 として表すことによって,ひずみエネルギ密度関数
として表すことによって,ひずみエネルギ密度関数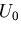 は,
は,
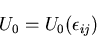 |
(297) |
負荷経路によらず現在のひずみであらわされる.
したがって,ひずみの状態量であるから全微分をとって,
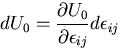 |
(298) |
のように考えて,
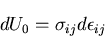 |
(299) |
したがって,
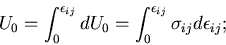 |
(300) |
のように負荷経路にそって積分して得られるものである.
一方,ひずみを応力の関数であるとして,
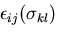 として表し,
として表し,
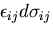 なる量を導入し,負荷経路にそって積分すると,
なる量を導入し,負荷経路にそって積分すると,
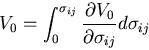 |
(302) |
となる.
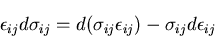 |
(303) |
なので,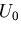 の存在が保証されるならば,
の存在が保証されるならば,
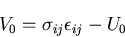 |
(304) |
という関係から導かれる.つまり,
応力ひずみ関係わかっていて,
上の式の右辺のひずみ成分を応力成分で表されることができれば,
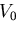 は,経路に依存しない状態量となる.
すなわち,
は,経路に依存しない状態量となる.
すなわち,
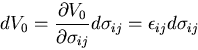 |
(305) |
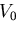 のことをコンプリメンタリひずみエネルギ密度関数
(complementary strain energy density function)
という.ひずみエネルギ密度関数の場合と同様に,
のことをコンプリメンタリひずみエネルギ密度関数
(complementary strain energy density function)
という.ひずみエネルギ密度関数の場合と同様に,
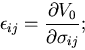 |
(306) |
| |
|
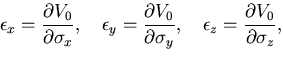 |
|
| |
|
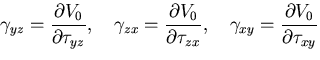 |
(307) |
の関係が導かれる.
これは,熱力学的ポテンシャル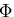 で温度やエントロピの変化を考えない場合の
式に当たる.
また,
で温度やエントロピの変化を考えない場合の
式に当たる.
また,
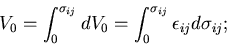 |
(308) |
応力ひずみ関係を考えると,
ポアソン比の範囲が,
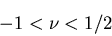 |
(311) |
なので,
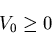 |
(312) |
である.
線形弾性体の場合には,
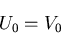 |
(313) |
である.しかしながら,
非線形弾性の場合について,例えば,棒の単軸引張を考える.この場合,
 |
(314) |
であり,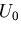 ,
,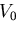 は,
は,
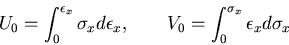 |
(315) |
である.
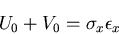 |
(316) |
の関係があるが,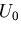 と
と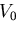 は,一般には等しくないことがわかる.
は,一般には等しくないことがわかる.
Figure 6.2:
ひずみエネルギ密度関数とコンプリメンタリひずみエネルギ密度関数
 |
図6.2から明かなように,
長方形部分の面積を表すのに 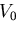 は,
は,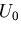 に対して
相補的(補足的)
(complementary) である.これが,"コンプリメンタリ"といわれる
ゆえんである.
に対して
相補的(補足的)
(complementary) である.これが,"コンプリメンタリ"といわれる
ゆえんである.
Akihiro Nakatani
2001-06-25
![]() 方向の変位を
方向の変位を ![]() とすると,
とすると,
![]() だけ離れた
面EFGHの変位は,
だけ離れた
面EFGHの変位は,
![]() となる.また,面ABCDの垂直応力
となる.また,面ABCDの垂直応力![]() は,
面EFGHでは,
は,
面EFGHでは,
![]() したがって応力0の状態から,これらの応力にいたるまでになす仕事を
考える.
変位が
したがって応力0の状態から,これらの応力にいたるまでになす仕事を
考える.
変位が![]() は,時刻
は,時刻![]() の時に,その値がわかっているものとし,
すなわち,
の時に,その値がわかっているものとし,
すなわち,
![]() の様に
時間
の様に
時間![]() に比例して変化するものとすると,仕事は,
に比例して変化するものとすると,仕事は,
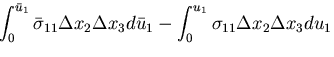
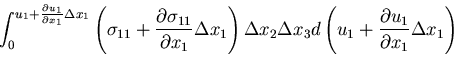
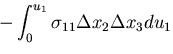
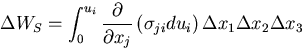
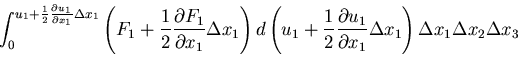
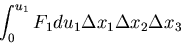
![$\displaystyle \left[\int_0^{u_i}\frac{\partial}{\partial x_j}\left(\sigma_{ji}du_i\right) + \int_0^{u_i}F_idu_i\right] \Delta x_1 \Delta x_2 \Delta x_3$](img716.gif)
![$\displaystyle \left[\int_0^{u_i}\left\{\left(%%
\frac{\partial\sigma_{ji}}{\par...
...{\partial(d u_i)}{\partial x_j}\right\}\right]
\Delta x_1 \Delta x_2 \Delta x_3$](img717.gif)
![$\displaystyle \left[\int_0^{u_i}\left\{\left(%%
\frac{\partial\sigma_{ji}}{\par...
...u_j)}{\partial x_i}%%
\right)\right\}\right]%%
\Delta x_1 \Delta x_2 \Delta x_3$](img718.gif)
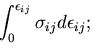
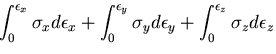
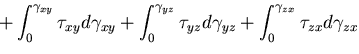
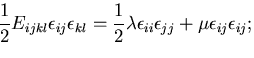
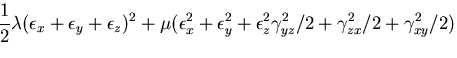
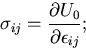
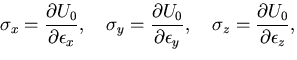
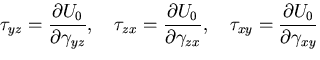
![]() として表すことによって,ひずみエネルギ密度関数
として表すことによって,ひずみエネルギ密度関数![]() は,
は,
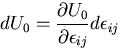
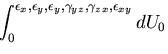
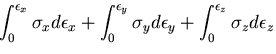
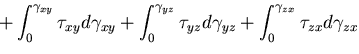
![]() として表し,
として表し,
![]() なる量を導入し,負荷経路にそって積分すると,
なる量を導入し,負荷経路にそって積分すると,
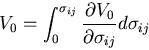
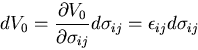
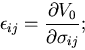
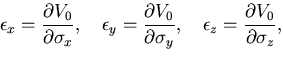
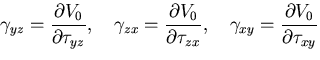
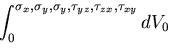
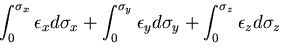
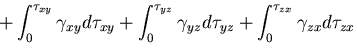
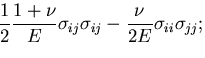
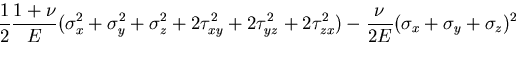
![]() は,
は,![]() に対して
相補的(補足的)
(complementary) である.これが,"コンプリメンタリ"といわれる
ゆえんである.
に対して
相補的(補足的)
(complementary) である.これが,"コンプリメンタリ"といわれる
ゆえんである.