応力で表した適合方程式

適合方程式

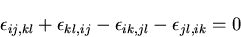$$\epsilon_{ij,kl}+\epsilon_{kl,ij}-\epsilon_{ik,jl}-\epsilon_{jl,ik}=0$$ (273)

に，応力ひずみ関係

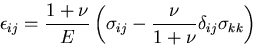$$\epsilon_{ij}=\frac{1+\nu}{E}\left(\sigma_{ij} -\frac{\nu}{1+\nu}\delta_{ij}\sigma_{kk}\right)$$ (274)

を代入し，変形すると， 応力で表した適合方程式

$$\sigma_{ij,kk}+\frac{1}{1+\nu}\sigma_{kk,ij} =\rho\left[-\frac{\nu}{1-\nu}\delta_{ij}g_{k,k}-(g_{i,j}+g_{j,i})\right]$$ (275)

を得る． これを，ベルトラミ・ミッチェルの適合方程式 (Beltrami-Michell's compatibility equation)と呼ぶ． 15個の方程式を解く代わりにこの6個の方程式から出発する方法を 応力法(force method)と呼ぶ． さらに，物体力が調和方程式を満たすポテンシャルから導かれる場合には， 応力は

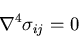$$\nabla^4\sigma_{ij}=0$$ (276)

の様に重調和関数となる． 一方，後で述べる二次元問題の解析で行われる エアリの応力関数 (Airy's stress function)を用いる 方法は，応力法の特別な例である．