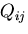 なる回転(座標変換)マトリクスでの変換
なる回転(座標変換)マトリクスでの変換
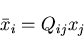 |
(234) |
を考えるえる.このとき,
弾性係数テンソル,ひずみテンソル,応力テンソルは次の変換を受ける
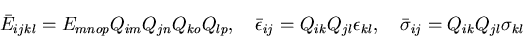 |
(235) |
まず,
![\begin{displaymath}
Q_{ij}=\left[\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]
\end{displaymath}](img606.gif) |
(236) |
を考えたとき,
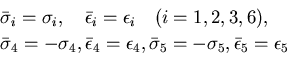 |
(237) |
である.
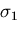 について,
について,
であり,一方,
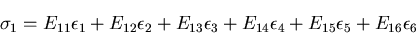 |
(240) |
であるから,任意の 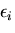 に対して
に対して
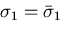 と
なるためには,
と
なるためには,
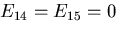 でなければならない.
でなければならない.
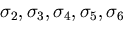 についても
同様な評価を行なうと,
についても
同様な評価を行なうと,
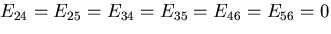 を得る.
を得る.
![\begin{displaymath}
\left[
\begin{array}{llllll}
E_{11} & E_{12} & E_{13} & 0 & ...
...column{2}{l}{{\rm Sym.}} & & & & E_{66} \\
\end{array}\right]
\end{displaymath}](img618.gif) |
(241) |
続いて,
![\begin{displaymath}
Q_{ij}=\left[\begin{array}{rrr}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]
\end{displaymath}](img619.gif) |
(242) |
を考えると
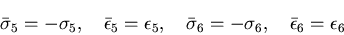 |
(243) |
から,
で,一方,
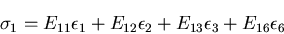 |
(246) |
なので,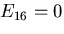 を得る.
同様に,
を得る.
同様に,
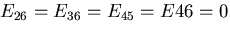 を得る.
これは,直交異方体
(orthotropic body)と呼ばれ9個の弾性定数で表わされる.
を得る.
これは,直交異方体
(orthotropic body)と呼ばれ9個の弾性定数で表わされる.
![\begin{displaymath}
\left[
\begin{array}{llllll}
E_{11} & E_{12} & E_{13} & 0 & ...
...column{2}{l}{{\rm Sym.}} & & & & E_{66} \\
\end{array}\right]
\end{displaymath}](img626.gif) |
(247) |
さらに,異方性の主軸が互いに等価であるとすると,
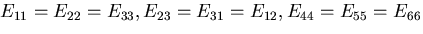 なる関係が成立するので,
なる関係が成立するので,
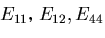 の3個の弾性定数で
表わされる.一般の立方晶(面心立方晶
(face center cubic crystal),
体心立方晶
(body center cubic crystal))の弾性定数は
このように3個で表わされる.
の3個の弾性定数で
表わされる.一般の立方晶(面心立方晶
(face center cubic crystal),
体心立方晶
(body center cubic crystal))の弾性定数は
このように3個で表わされる.
![\begin{displaymath}
\left[
\begin{array}{llllll}
E_{11} & E_{12} & E_{12} & 0 & ...
...column{2}{l}{{\rm Sym.}} & & & & E_{44} \\
\end{array}\right]
\end{displaymath}](img629.gif) |
(248) |
最後に,
![\begin{displaymath}
Q_{ij}=\left[\begin{array}{rrr}
\frac{1}{\sqrt{2}} & \frac{1...
...{2}} & \frac{1}{\sqrt{2}} & 0 \\
0 & 0 & 1
\end{array}\right]
\end{displaymath}](img630.gif) |
(249) |
を考えると,
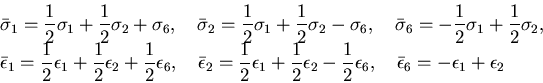 |
(250) |
なので,
ゆえに,
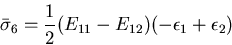 |
(253) |
一方,
比較すると,
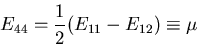 |
(257) |
ここで,
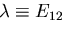 とおくと,
とおくと,
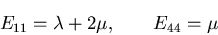 |
(258) |
と表わされる.
![\begin{displaymath}
\left[
\begin{array}{llllll}
\lambda+2\mu & \lambda & \lambd...
...
\multicolumn{2}{l}{{\rm Sym.}} & & & & \mu
\end{array}\right]
\end{displaymath}](img645.gif) |
(259) |
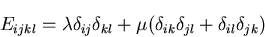 |
(262) |
この表式からわかるように,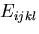 はもはやいかなる座標変換によっても
その値を変えない定数になっていることがわかる.
よって等方体の弾性定数は2個で表わされる.
この式をフックの法則
(Hooke's law)という.
ここで導入した
はもはやいかなる座標変換によっても
その値を変えない定数になっていることがわかる.
よって等方体の弾性定数は2個で表わされる.
この式をフックの法則
(Hooke's law)という.
ここで導入した 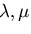 は,ラーメの定数(Lamé's constants)と
呼ばれる.
は,ラーメの定数(Lamé's constants)と
呼ばれる.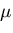 は,しばしば,
は,しばしば,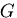 と書かれ,横弾性係数(shear modulus)
と呼ばれる.そのほかに,等方体の弾性定数には物理的意味を考慮して
ポアソン比(Poisson ratio)
と書かれ,横弾性係数(shear modulus)
と呼ばれる.そのほかに,等方体の弾性定数には物理的意味を考慮して
ポアソン比(Poisson ratio) 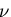 ,
ヤング率
(縦弾性係数)
(Young modulus)
,
ヤング率
(縦弾性係数)
(Young modulus) 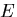 ,
体積弾性係数
(bulk modulus)
,
体積弾性係数
(bulk modulus) 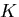 ,
などさまざまな量が定義されるが,
それらの量は以下のように,互いに独立な2つの量で記述される.
,
などさまざまな量が定義されるが,
それらの量は以下のように,互いに独立な2つの量で記述される.
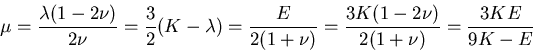 |
(264) |
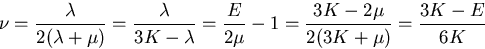 |
(265) |
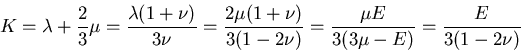 |
(267) |
ポアソン比が 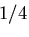 という
特殊な値の時には,
という
特殊な値の時には,
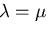 となり,弾性体の方程式はかなり簡単化される.
また,
となり,弾性体の方程式はかなり簡単化される.
また,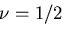 は,非圧縮性
(uncompressibility)を示す.
は,非圧縮性
(uncompressibility)を示す.
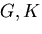 が正であるという条件から,ポアソン比は
が正であるという条件から,ポアソン比は
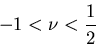 |
(268) |
でなければならない.
Akihiro Nakatani
2001-06-25
![\begin{displaymath}
Q_{ij}=\left[\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]
\end{displaymath}](img606.gif)
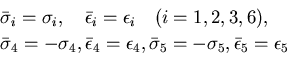
![\begin{displaymath}
\left[
\begin{array}{llllll}
E_{11} & E_{12} & E_{13} & 0 & ...
...column{2}{l}{{\rm Sym.}} & & & & E_{66} \\
\end{array}\right]
\end{displaymath}](img618.gif)
![\begin{displaymath}
Q_{ij}=\left[\begin{array}{rrr}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]
\end{displaymath}](img619.gif)
![\begin{displaymath}
\left[
\begin{array}{llllll}
E_{11} & E_{12} & E_{13} & 0 & ...
...column{2}{l}{{\rm Sym.}} & & & & E_{66} \\
\end{array}\right]
\end{displaymath}](img626.gif)
![\begin{displaymath}
\left[
\begin{array}{llllll}
E_{11} & E_{12} & E_{12} & 0 & ...
...column{2}{l}{{\rm Sym.}} & & & & E_{44} \\
\end{array}\right]
\end{displaymath}](img629.gif)
![\begin{displaymath}
Q_{ij}=\left[\begin{array}{rrr}
\frac{1}{\sqrt{2}} & \frac{1...
...{2}} & \frac{1}{\sqrt{2}} & 0 \\
0 & 0 & 1
\end{array}\right]
\end{displaymath}](img630.gif)
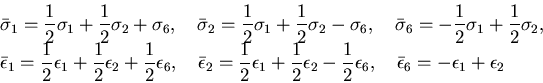
![\begin{displaymath}
\left[
\begin{array}{llllll}
\lambda+2\mu & \lambda & \lambd...
...
\multicolumn{2}{l}{{\rm Sym.}} & & & & \mu
\end{array}\right]
\end{displaymath}](img645.gif)
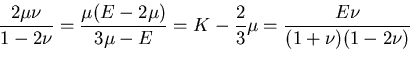
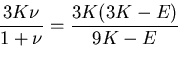
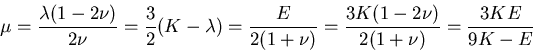
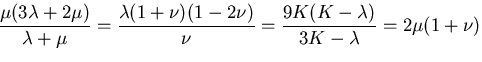
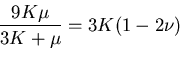
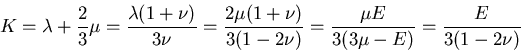
![]() という
特殊な値の時には,
という
特殊な値の時には,
![]() となり,弾性体の方程式はかなり簡単化される.
また,
となり,弾性体の方程式はかなり簡単化される.
また,![]() は,非圧縮性
(uncompressibility)を示す.
は,非圧縮性
(uncompressibility)を示す.
![]() が正であるという条件から,ポアソン比は
が正であるという条件から,ポアソン比は