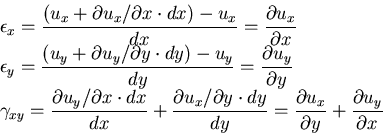基準配置で,点Qが点Pの極近傍にあるとし,
点Qの座標を
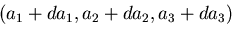 とおくことにする.
現配置では,点Qは,Q
とおくことにする.
現配置では,点Qは,Q 座標
座標
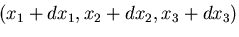 に運動したとする.
点Pと点P
に運動したとする.
点Pと点P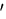 は本来物体中の同一の点であるから
は本来物体中の同一の点であるから
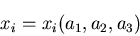 |
(170) |
のように1対1の対応関係にあるので,
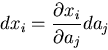 |
(171) |
となる.
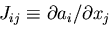 は,
ヤコビ行列(Jacobian matrix)と呼ばれる.
さて,ここで,2点PQの距離を
は,
ヤコビ行列(Jacobian matrix)と呼ばれる.
さて,ここで,2点PQの距離を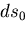 , 2点P
, 2点P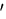 Q
Q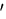 の距離を
の距離を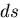 とすると,
とすると,
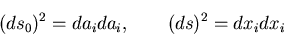 |
(172) |
となるので,これらの差をとり,式(4.3)を用いると,
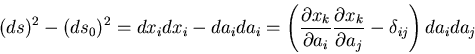 |
(173) |
ここで,
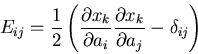 |
(174) |
とおくと,
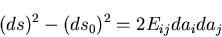 |
(175) |
となる.上の式の左辺はスカラーであり,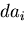 ,
, 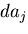 がベクトルであるから,
がベクトルであるから,
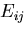 はテンソルである.
さて,
はテンソルである.
さて,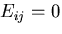 の時には,
の時には,
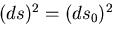 を意味するので,変形のものさしとして,
を意味するので,変形のものさしとして,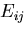 を用いることができる.
これをひずみテンソル
(strain tensor)とよぶ.
を用いることができる.
これをひずみテンソル
(strain tensor)とよぶ.
式(4.2)を用いて書き下すと,
と表すことができる.
さて,以上の議論は,長さの2乗の変化を変形前の座標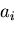 で表したものである.
この様にして定義されるひずみテンソル
で表したものである.
この様にして定義されるひずみテンソル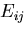 のことをとくに
Greenのひずみテンソル
または,Lagrange のひずみテンソル
という.
のことをとくに
Greenのひずみテンソル
または,Lagrange のひずみテンソル
という.
一方,逆関係
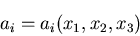 |
(177) |
が成り立つとし,式(4.3)のかわりに,
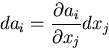 |
(178) |
を用いて,
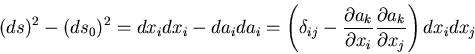 |
(179) |
を得る.ここで,
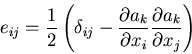 |
(180) |
とおくと,
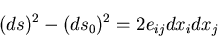 |
(181) |
このように,現配置の座標で表した場合のひずみテンソル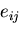 のことを
Almansi のひずみテンソル
または,Eulerのひずみテンソル
という.
のことを
Almansi のひずみテンソル
または,Eulerのひずみテンソル
という.
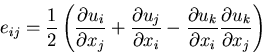 |
(182) |
さて,
 |
(183) |
であるが,変位や変位の勾配が小さい時には,
変位の勾配の2次の項は無視できるので,
Green-Lagrange のひずみと,Almansi-Euler のひずみの区別はなくなる.
すなわち,
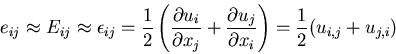 |
(184) |
このように微小変形理論
(infinitesimal theory)で得られるひずみテンソル,
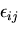 をCauchy の 微小ひずみテンソル
(Cauchy's strain tensor)
とよび,以後,単にひずみテンソルとよぶことにする.
ここで述べたすべてのひずみテンソルは,
その定義から明かなように対称テンソルであり,
をCauchy の 微小ひずみテンソル
(Cauchy's strain tensor)
とよび,以後,単にひずみテンソルとよぶことにする.
ここで述べたすべてのひずみテンソルは,
その定義から明かなように対称テンソルであり,
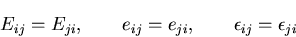 |
(185) |
がなりたつ.
具体的に, を用いて書くと,
を用いて書くと,
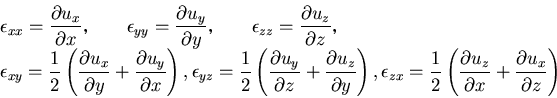 |
(186) |
と表される.
さて,
ひずみテンソルの工学的意味を明かにするために,
まず,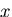 軸方向の単軸引張変形を考える.
軸方向の単軸引張変形を考える.
Figure 4.2:
棒の引張変形
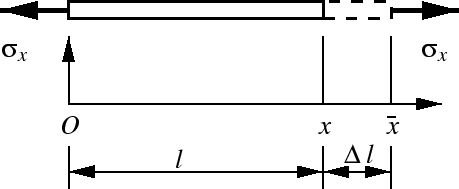 |
原点が固定されていて長さ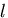 の棒が,
の棒が,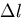 だけ伸びたとき,
座標
だけ伸びたとき,
座標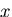 の点での変位は,
の点での変位は,
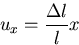 |
(187) |
ゆえに,
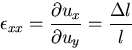 |
(188) |
一方,材料力学などでひずみを
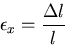 |
(189) |
と定義しているから,
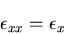 |
(190) |
となる.同様に考えて,一般に
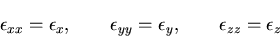 |
(191) |
と書ける.
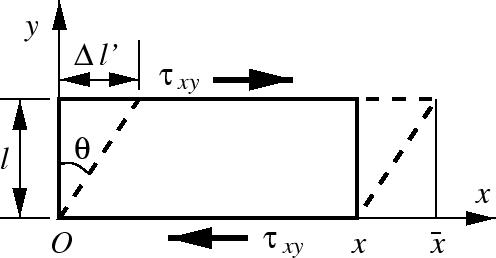
次に,高さ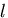 のブロックが,せん断応力を受けて微小な角度
のブロックが,せん断応力を受けて微小な角度 だけ
せん断変形を受ける場合を考える.
だけ
せん断変形を受ける場合を考える.
Figure 4.3:
ブロックのせん断変形
 |
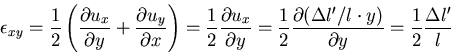 |
(192) |
となる.
一方,材料力学の基礎では,
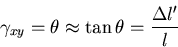 |
(193) |
したがって,
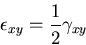 |
(194) |
さらに一般的には,
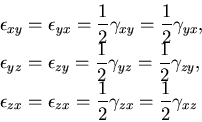 |
(195) |
このように,ひずみテンソルのせん断成分は,
角度の変化で表される工学ひずみ
(engineering strain)の半分の値を持つ.
このような工学ひずみを用いてひずみ-変位関係
(strain-displacement relation)を次のようにおく.
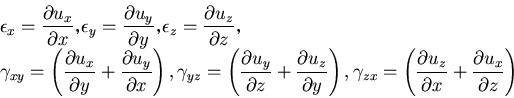 |
(196) |
工学ひずみにおいても明かに対称性がある.
[例]
変形前に, の稜をもつ直方体が,図のように変形後
平行六面体になった場合を考えて,工学ひずみ-変位関係を導く.
の稜をもつ直方体が,図のように変形後
平行六面体になった場合を考えて,工学ひずみ-変位関係を導く.
Figure 4.4:
微小直方体の変形
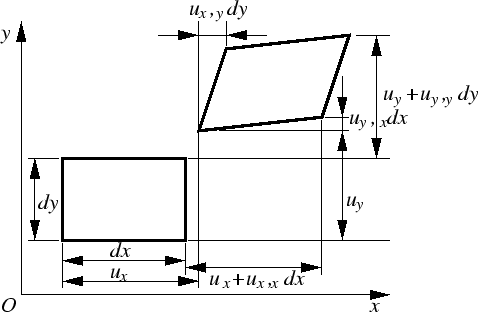 |
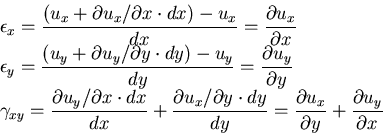 |
(197) |
同様にして,
 も得られる.
も得られる.
Akihiro Nakatani
2001-06-25
![]() とおくことにする.
現配置では,点Qは,Q
とおくことにする.
現配置では,点Qは,Q![]() 座標
座標
![]() に運動したとする.
点Pと点P
に運動したとする.
点Pと点P![]() は本来物体中の同一の点であるから
は本来物体中の同一の点であるから
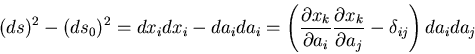
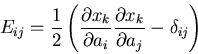
![$\displaystyle \frac{1}{2}\left[
\left(\frac{\partial u_k}{\partial a_i}+\delta_...
...
\left(\frac{\partial u_k}{\partial a_j}+\delta_{kj}\right)
-\delta_{ij}\right]$](img468.gif)
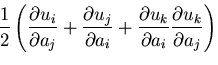
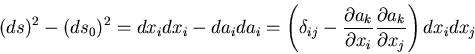
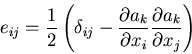
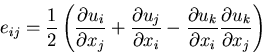
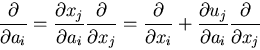
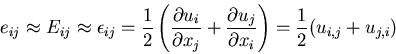
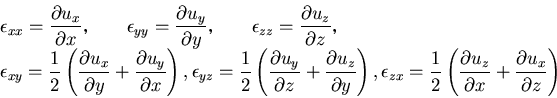
![]() 軸方向の単軸引張変形を考える.
軸方向の単軸引張変形を考える.
![]() の棒が,
の棒が,![]() だけ伸びたとき,
座標
だけ伸びたとき,
座標![]() の点での変位は,
の点での変位は,
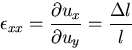
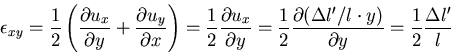
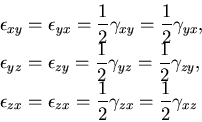
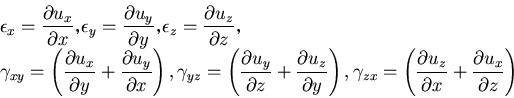
![]() の稜をもつ直方体が,図のように変形後
平行六面体になった場合を考えて,工学ひずみ-変位関係を導く.
の稜をもつ直方体が,図のように変形後
平行六面体になった場合を考えて,工学ひずみ-変位関係を導く.