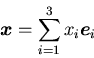ベクトル(vector)は,大きさと向きを持つ量である.長さ1のベク
トルは,単位ベクトル(unit vector)と呼ばれる.一般に,3次元空
間の任意のベクトルは,3つの独立なベクトルの線形結合で表され
る.さらに,基底ベクトル(base vector)は,この3つの独立なベク
トルに単位ベクトルを用いたもので,
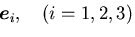 で表すとする.
で表すとする.
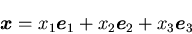 |
(7) |
と書き表すことができる.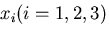 は,
は,
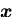 の成分
(component)と呼ばれ,ある座標系がきまれば,ベクトル
の成分
(component)と呼ばれ,ある座標系がきまれば,ベクトル
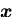 を
を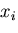 と表示できる.前者を,記号表示,後者を,指標表示とい
う.上の式は,
と表示できる.前者を,記号表示,後者を,指標表示とい
う.上の式は,
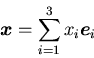 |
(8) |
と書くことができる.3次元ユークリッド空間では,和は1,2,3の範
囲で取られるので,和の記号を取り去り,
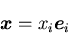 |
(9) |
と書く.つまり,「一つの項の中に同じ添字(suffix)が,2度現われた場合,
その添字について和をとる」という規則を総和規約(summation
convention)という.
和をとる添字は,疑標(dummy index)と呼ばれ,項の中だけで,通
常他の文字と置き換えが可能である.それに対して,和をとらない
添字は自由標(free index)と呼ばれる.
『ポイント』指標表示と総和規約に関する注意
- 総和を取るという約束以外は,指標記号を用いている場合
には,通常の四則演算にしたがうので,交換法則や結合法則が使
える.
- 丁寧に書けば,ベクトルは成分と基底ベクトルの積の線形
結合で表されるが,成分だけで表示する場合が多い.
- 同じ項の中の添字が現われる回数は,1回または,2回であ
る.たとえば,
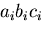 は3回でてくるので誤りである.2回で
てくれば,擬標として扱い総和規約によって和をとる.1回ならば
自由標であるので,和をとらない.
は3回でてくるので誤りである.2回で
てくれば,擬標として扱い総和規約によって和をとる.1回ならば
自由標であるので,和をとらない.
- 同一項に2度現われる擬標は項ごとに別の文字に置き換え
可能であるが,すでに添字として使っている文字はその置き換えで
使ってはならない.
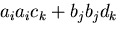 を
を
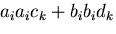 とか,
とか,
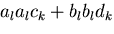 とか,
とか,
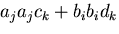 とかに置き換えるのは良いが,
とかに置き換えるのは良いが,
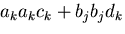 に置き換えるのは誤りである.
に置き換えるのは誤りである.
- 自由標がある場合には,左辺および右辺の全ての項に同じ
自由標が必ず含まれていなければならない.
- 自由標を置き換える場合には,式全体で(左辺と右辺とも
に)全ての自由標を別の文字に置き換えることはできるが,特定の
項のみの添字は勝手に他の文字に変えてはならない(ただし,特定
の成分に対して成り立つ式であることが注釈として与えられている
場合には,置き換えることができないが,普通そのような式はエレ
ガントさに欠けるので使われないはずである).
- 自由標を置き換える場合にも,すでに添字として使ってい
る文字は置き換えに使ってはいけない.
- 総和規約を使っている式を他の式に代入する場合には,上
の約束に従って,文字を置き換えることが多い.
- 総和規約に従わない添字は,括弧( )でくくるなどで区別
するのが良いでしょう.
Akihiro Nakatani
2001-06-25
![]() で表すとする.
で表すとする.