Next: ベクトルの座標変換 Up: ベクトルとテンソル解析入門 Previous: ベクトルの内積とクロネッカーのデルタ Contents Index
二つのベクトル
![]() と
と
![]() の外積(ベクトル積)は,
の外積(ベクトル積)は,
![]() と表記され,両ベクトルのなす角
と表記され,両ベクトルのなす角![]() と,両ベクトルが作る平行四辺形の面に垂直で,
と,両ベクトルが作る平行四辺形の面に垂直で,
![]() から
から
![]() に向かって右ねじを回すときのねじの進む方向に向く単
位ベクトル
に向かって右ねじを回すときのねじの進む方向に向く単
位ベクトル
![]() によって,
によって,
| (13) |
| (14) |
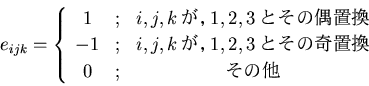 |
(15) |
二つのベクトル
![]() と
と
![]() の外積(ベクトル積)によって
得られるベクトルを
の外積(ベクトル積)によって
得られるベクトルを
![]() とすると,
とすると,
| (16) |
| (17) |
『ポイント』 交代記号に関して
| (18) |
| (19) |
| (20) | |||
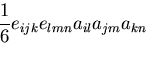 |
(21) |
| (22) |
| (23) |
| (24) |
| (25) |
Akihiro Nakatani 2001-06-25