Next: サンブナンのねじり問題 Up: ねじり問題 Previous: サンブナンの原理 Contents Index
| (496) |
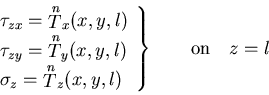 |
(497) |
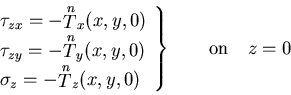 |
(498) |
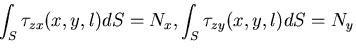 |
|||
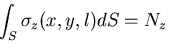 |
|||
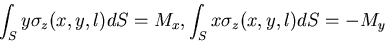 |
|||
![$\displaystyle \int_{S}[x\tau_{zy}(x, y, l)-y\tau_{zx}(x, y, l)] dS = M_z$](img1209.gif) |
(499) |
St. Venant の問題は,重ね合わせの原理を用いることにより,
[I] 軸方向の力![]() による棒の引張圧縮
による棒の引張圧縮
[II] 端面と平行な面内の![]() 軸まわりの
曲げモーメント
軸まわりの
曲げモーメント ![]() および,
および,![]() による曲げ
による曲げ
[III] 端面に垂直な面![]() 軸まわりのねじりモーメント
軸まわりのねじりモーメント![]() によるねじり
によるねじり
[IV] 端面内の力 ![]() および,
および,![]() によるせん断と曲げ
によるせん断と曲げ
の4種の問題に分解される.
[I], [II] の問題に対する解は,応力の成分のうち0でないものは,
![]() のみであり,材料力学で学んだ通りの結果を与える.次節以降で
は,[III]の問題について考える.[IV]の問題については,本講義では省略す
ることにする.
のみであり,材料力学で学んだ通りの結果を与える.次節以降で
は,[III]の問題について考える.[IV]の問題については,本講義では省略す
ることにする.
Akihiro Nakatani 2001-06-25