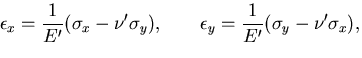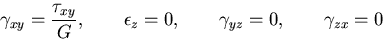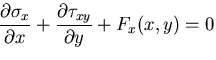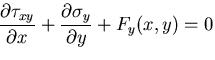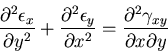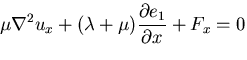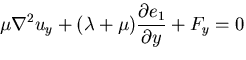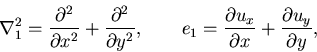直角座標系 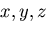 において,変位ベクトル
において,変位ベクトル
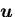 の成分
のうち,たとえば
の成分
のうち,たとえば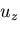 がいたるところ0であり,他の成分
がいたるところ0であり,他の成分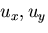 が,座標
が,座標 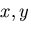 のみの関数であるとき,平面ひずみ
(plane strain)の状態にある
という.すなわち,
のみの関数であるとき,平面ひずみ
(plane strain)の状態にある
という.すなわち,
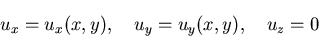 |
(375) |
このとき,ひずみが零でないものは,
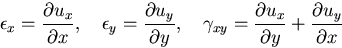 |
(376) |
であり,これらは,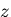 に無関係となる.
に無関係となる.
さて,応力ひずみ関係は,
| |
|
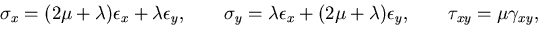 |
|
| |
|
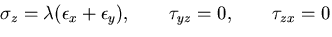 |
(377) |
または,
| |
|
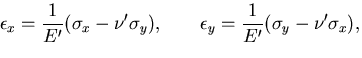 |
|
| |
|
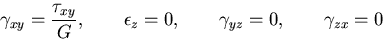 |
(378) |
ここで,
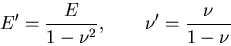 |
(379) |
とおいている.
また,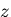 方向の変位は零であるがその方向の応力
方向の変位は零であるがその方向の応力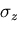 は零でなく,
は零でなく,
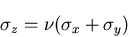 |
(380) |
となる.
一方,応力のつりあい方程式は,
また,ひずみの適合方程式は,
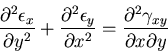 |
(382) |
平面ひずみ状態におけるナビアの方程式は,
| |
|
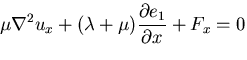 |
|
| |
|
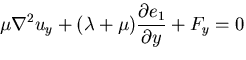 |
(383) |
ここで,
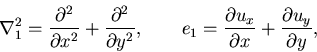 |
(384) |
である.
さて,いま,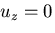 を仮定しているが,ここで,
を仮定しているが,ここで,
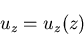 |
(385) |
のように,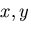 に依存しない軸方向変位を許すものとする.
このとき,物体力を0とおいたナビアの方程式は,
に依存しない軸方向変位を許すものとする.
このとき,物体力を0とおいたナビアの方程式は,
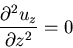 |
(386) |
なので,
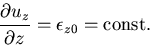 |
(387) |
となる.
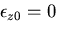 のときには上で述べた平面ひずみになるが,
のときには上で述べた平面ひずみになるが,
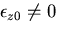 のときには平面ひずみの解に,
のときには平面ひずみの解に,
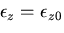 を加え合わせればよいことになる.
このような状態を一般化した平面ひずみ
(generalized plane strain)状態という.
を加え合わせればよいことになる.
このような状態を一般化した平面ひずみ
(generalized plane strain)状態という.
Akihiro Nakatani
2001-06-25
![]() において,変位ベクトル
において,変位ベクトル
![]() の成分
のうち,たとえば
の成分
のうち,たとえば![]() がいたるところ0であり,他の成分
がいたるところ0であり,他の成分![]() が,座標
が,座標 ![]() のみの関数であるとき,平面ひずみ
(plane strain)の状態にある
という.すなわち,
のみの関数であるとき,平面ひずみ
(plane strain)の状態にある
という.すなわち,