- 図1のようなL型の棒の点A,Bに集中荷重
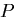 ,
, 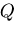 が作用しているとき,
着力点の荷重方向のたわみ
が作用しているとき,
着力点の荷重方向のたわみ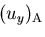 ,
, 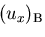 を
カスチリアノの定理を用いて求めなさい.
ただし,材料のヤング率,横弾性係数,断面積,断面2次モーメントをそれぞれ,
を
カスチリアノの定理を用いて求めなさい.
ただし,材料のヤング率,横弾性係数,断面積,断面2次モーメントをそれぞれ,
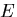 ,
, 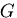 ,
, 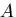 ,
, 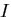 とする.
とする.
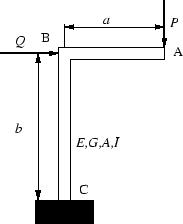
図1
- 図2に示すような静定トラスの点Bに,集中荷重
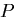 が垂直下方に作
用しているとする.ここで,各棒は断面積
が垂直下方に作
用しているとする.ここで,各棒は断面積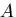 ,ヤング率
,ヤング率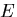 の同一材料である.
の同一材料である.
- (1)
- 点Bでの水平変位
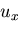 と,垂直変位
と,垂直変位 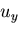 を
仮想仕事の原理を用いて求めなさい.
を
仮想仕事の原理を用いて求めなさい.
- (2)
- 点Bでの垂直変位
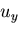 を
カスチリアノの定理を用いて求めなさい.
を
カスチリアノの定理を用いて求めなさい.
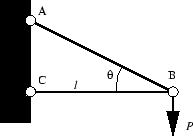
図2
- 図3に示すような中央に集中荷重
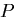 の作用する
両端固定はりのたわみ
の作用する
両端固定はりのたわみ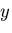 を,求めることを考える.
を,求めることを考える.
- (1)
- 材料力学のはりの理論に基づいた
方法(どんな方法でも良い)を用いてたわみの式
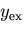 と荷重点の
たわみ
と荷重点の
たわみ
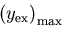 を求めなさい(これを厳密解とする).
を求めなさい(これを厳密解とする).
- (2)
- カスチリアノの定理を用いて
荷重点のたわみ
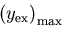 を求めなさい.
を求めなさい.
- (3)
- 両端でたわみとたわみ角が零であるという境界条件を満足し,
かつ,問題の対称性を考慮すると,
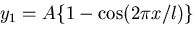 を近似解と仮定してもよさそうである.
このとき,最小ポテンシャルエネルギの原理を用いて,たわみ曲線の近似式を
決定しなさい(すなわち
を近似解と仮定してもよさそうである.
このとき,最小ポテンシャルエネルギの原理を用いて,たわみ曲線の近似式を
決定しなさい(すなわち 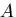 の値を決定する).
また,この時のポテンシャルエネルギ
の値を決定する).
また,この時のポテンシャルエネルギ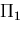 と
荷重点のたわみ
と
荷重点のたわみ
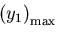 を求めなさい.
を求めなさい.
- (4)
-
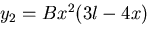 を荷重点の左側のたわみを表す式として用い,
荷重点右側には,これと対称な式を用いると,
両端でたわみとたわみ角が零であるという境界条件を満足し,
かつ,たわみ角の連続性が保証されるので,
この式を近似解と仮定してもよさそう
である.
このとき,最小ポテンシャルエネルギの原理を用いて,たわみ曲線の近似式を
決定しなさい(すなわち
を荷重点の左側のたわみを表す式として用い,
荷重点右側には,これと対称な式を用いると,
両端でたわみとたわみ角が零であるという境界条件を満足し,
かつ,たわみ角の連続性が保証されるので,
この式を近似解と仮定してもよさそう
である.
このとき,最小ポテンシャルエネルギの原理を用いて,たわみ曲線の近似式を
決定しなさい(すなわち 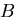 の値を決定する).
また,この時のポテンシャルエネルギ
の値を決定する).
また,この時のポテンシャルエネルギ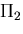 と
荷重点のたわみ
と
荷重点のたわみ
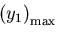 を求めなさい.
を求めなさい.
- (5)
-
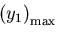 ,
,
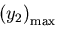 と
と
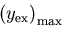 を比較しなさい.
また,
を比較しなさい.
また,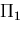 ,
,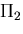 の大小関係を調べて,どちらが正解に近いかを
について論じなさい.
の大小関係を調べて,どちらが正解に近いかを
について論じなさい.
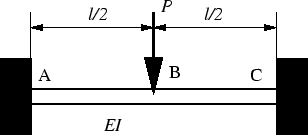
図3
- 図4に示すような3次元物体の2点A,Bに向きが反対で大きさの等しい集中荷重
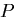 が加えられてつりあっている時,相反定理を用いて体積変化を求め
なさい.
が加えられてつりあっている時,相反定理を用いて体積変化を求め
なさい.
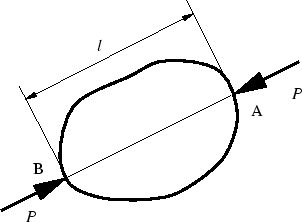
図4
Akihiro Nakatani
2001-06-25



