コーシーの関係からも明かなように,法線
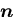 を持つ面に作用する応力ベクトル
を持つ面に作用する応力ベクトル
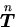 は,
は,
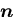 の方向に依存する.したがって,ある面を選べば,その面に対しては,
応力ベクトルが垂直になることが考えられる.このような面を
主面
(principal plane), その法線を主軸
(principal axis),あるいは,法線方向を
主方向(principal direction),
さらに,主面に作用する垂直応力を主応力
(principal stress)とよぶ.
主軸方向の単位ベクトルを
の方向に依存する.したがって,ある面を選べば,その面に対しては,
応力ベクトルが垂直になることが考えられる.このような面を
主面
(principal plane), その法線を主軸
(principal axis),あるいは,法線方向を
主方向(principal direction),
さらに,主面に作用する垂直応力を主応力
(principal stress)とよぶ.
主軸方向の単位ベクトルを
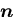 ,対応する主応力を
,対応する主応力を 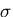 と
すると,主面に作用する応力ベクトルは,
と
すると,主面に作用する応力ベクトルは,
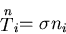 |
(153) |
となり,垂直応力の成分だけとなる.
一方,このベクトルは,任意の面の応力テンソルによって
コーシーの関係
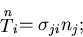 |
(154) |
のように表されるので,
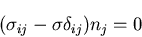 |
(155) |
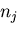 が0でない非自明解を持つためには,
が0でない非自明解を持つためには,
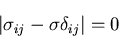 |
(156) |
となる.これを展開すると,
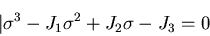 |
(157) |
ここで,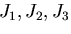 は,
は,
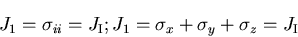 |
(158) |
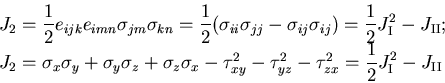 |
(159) |
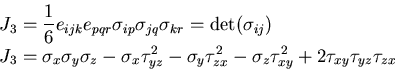 |
(160) |
である.ただし,
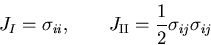 |
(161) |
一方,この関係式の解を
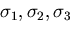 とすると,
とすると,
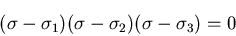 |
(162) |
なので,解と係数の関係より,
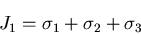 |
(163) |
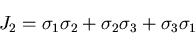 |
(164) |
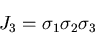 |
(165) |
主応力
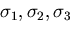 および,
および,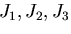 ,
,
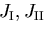 は,任意の点の応力の状態を規定するものであり,
座標系のとり方に依存しない,
これらを応力の不変量
(invariant)とよび
とくに
は,任意の点の応力の状態を規定するものであり,
座標系のとり方に依存しない,
これらを応力の不変量
(invariant)とよび
とくに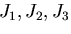 ,を主不変量
(principal invariant)とよぶ.
,を主不変量
(principal invariant)とよぶ.
Akihiro Nakatani
2001-06-25
![]() を持つ面に作用する応力ベクトル
を持つ面に作用する応力ベクトル
![]() は,
は,
![]() の方向に依存する.したがって,ある面を選べば,その面に対しては,
応力ベクトルが垂直になることが考えられる.このような面を
主面
(principal plane), その法線を主軸
(principal axis),あるいは,法線方向を
主方向(principal direction),
さらに,主面に作用する垂直応力を主応力
(principal stress)とよぶ.
主軸方向の単位ベクトルを
の方向に依存する.したがって,ある面を選べば,その面に対しては,
応力ベクトルが垂直になることが考えられる.このような面を
主面
(principal plane), その法線を主軸
(principal axis),あるいは,法線方向を
主方向(principal direction),
さらに,主面に作用する垂直応力を主応力
(principal stress)とよぶ.
主軸方向の単位ベクトルを
![]() ,対応する主応力を
,対応する主応力を ![]() と
すると,主面に作用する応力ベクトルは,
と
すると,主面に作用する応力ベクトルは,
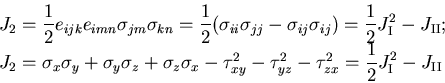
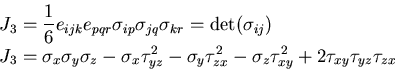
![]() および,
および,![]() ,
,
![]() は,任意の点の応力の状態を規定するものであり,
座標系のとり方に依存しない,
これらを応力の不変量
(invariant)とよび
とくに
は,任意の点の応力の状態を規定するものであり,
座標系のとり方に依存しない,
これらを応力の不変量
(invariant)とよび
とくに![]() ,を主不変量
(principal invariant)とよぶ.
,を主不変量
(principal invariant)とよぶ.