物体中にとった稜の長さが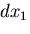 ,
,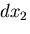 ,
,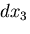 なる微小直六面体を
考えよう.面 ABCD にはたらく応力を
なる微小直六面体を
考えよう.面 ABCD にはたらく応力を 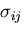 とすると,
面 EFGH の応力は,
とすると,
面 EFGH の応力は,
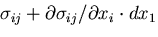 となる.他の方向についても同様な応力が考えられる.
いま,この直六面体の重心を通る
となる.他の方向についても同様な応力が考えられる.
いま,この直六面体の重心を通る 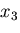 軸まわりのモーメントの
つりあいを考えると,
軸まわりのモーメントの
つりあいを考えると,
を得るが,高次項を省略すると,
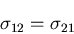 |
(137) |
となる.同様のことは,他のせん断応力についてもいうことができ,
一般に次の関係が成り立つ.
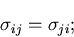 |
(138) |
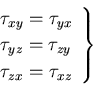 |
(139) |
これは,直交する2つの面にはたらくせん断応力についての
重要な関係であり,せん断応力の対称性
(symmetry)あるいは,共役性という.
次に,微小直六面体における力のつり合いを考えてみよう.
物体が均質であるとして,
単位体積当たりの物体力を
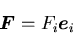 |
(140) |
とする.
このとき,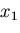 方向の力のつりあいは,
方向の力のつりあいは,
となるので,つぎの関係が得られる.
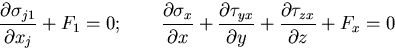 |
(142) |
同様な関係は,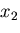 方向,および,
方向,および,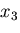 方向の力のつりあいを
考えることによって得られるが,応力の対称性を考慮して
これらをまとめると,次のように表される.
方向の力のつりあいを
考えることによって得られるが,応力の対称性を考慮して
これらをまとめると,次のように表される.
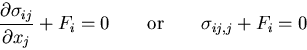 |
(143) |
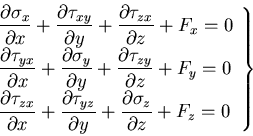 |
(144) |
これは,応力の平衡方程式
(equilibrium equation) あるいは,
つりあい方程式
と呼ばれ,弾性力学において最も重要な関係のひとつである.
[例題3.2]
運動保存則
(conservation law of momentum=Eulelr の第1法則)
および角運動量保存則
(conservation moment of momentum=Eulelr の第2法則)
を用いて,応力の平衡方程式およ応力の対称性を導く.
物体が静的つりあい状態にあるとき,これはすなわち,
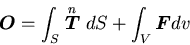 |
(145) |
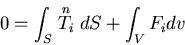 |
(146) |
であるが,コーシーの関係を用いて,第1項の表面力を応力で表し,
Gaussの発散定理を用いると.
![\begin{displaymath}
\left.
\begin{array}{rcl}
\mbox{\boldmath$O$}
& = & \displ...
...style\int_{v}[(\sigma_{ij})_{,j} + F_i] dv
\end{array}\right\}
\end{displaymath}](img401.gif) |
(147) |
となる.上式が常に成り立つためには,
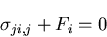 |
(148) |
を得る.
角運動量保存則は,角運動量の変化率は合モーメントに等しいことを意味するから,
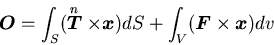 |
(149) |
すなわち,
ところで,第1項は 0 であり,
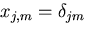 であるから,
結局,
であるから,
結局,
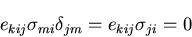 |
(151) |
となり,これから,
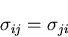 |
(152) |
を得る.
Akihiro Nakatani
2001-06-25
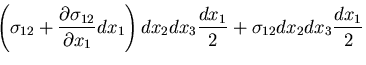
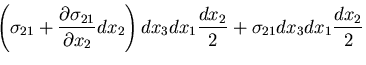
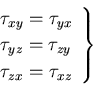
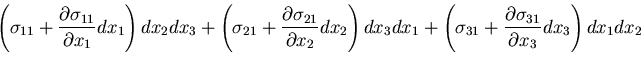
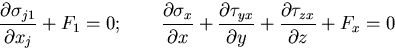
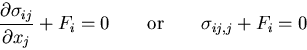
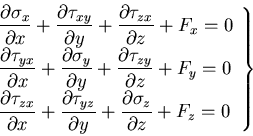
![\begin{displaymath}
\left.
\begin{array}{rcl}
\mbox{\boldmath$O$}
& = & \displ...
...style\int_{v}[(\sigma_{ij})_{,j} + F_i] dv
\end{array}\right\}
\end{displaymath}](img401.gif)
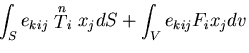
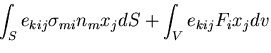
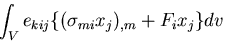
![$\displaystyle \int_{V} e_{kij}[(\sigma_{mi,m}+F_i) x_j + \sigma_{mi}x_{j,m}] dv$](img408.gif)