Next: 発散定理に関連するまとめ Up: ベクトルの発散定理 Previous: ベクトルの発散定理 Contents Index
点P(![]() )を,1頂点として,
)を,1頂点として,
![]() ,
, ![]() ,
, ![]() の長さの辺を持つ直方体を
の長さの辺を持つ直方体を ![]() とし
て,ガウスの発散定理を適用してみる.
ベクトル
とし
て,ガウスの発散定理を適用してみる.
ベクトル
![]() は,直方体内
で,
は,直方体内
で,
![]() ,
,
![]() ,
,
![]() のように変化し,また,
のように変化し,また,![]() ,
, ![]() ,
, ![]() 軸に垂直な面の法線
ベクトルは,それぞれ,
軸に垂直な面の法線
ベクトルは,それぞれ,
![]() ,
, ![]() ,
,
![]() ,辺の面積は,
,辺の面積は,
![]() ,
,
![]() ,
,
![]() であるから,高次の微小量を無視すると,
であるから,高次の微小量を無視すると,
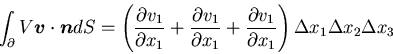 |
(110) |
| (111) |
| (112) |