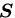 が,4個の指標を持つ81個の成分
が,4個の指標を持つ81個の成分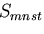 と,
と,
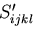 で表されるとき,
で表されるとき,
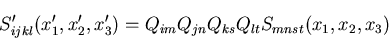 |
(79) |
のように関係づけられるならば,
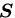 は4階のテンソル(fourth order
tensor)であるという.
一般に,
は4階のテンソル(fourth order
tensor)であるという.
一般に,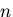 階のテンソルは,
階のテンソルは,
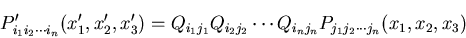 |
(80) |
で定義される.スカラーは,0階のテンソル(zero order tensor)と
もいい,ベクトルは,1階のテンソル(first order tensor)ともい
う.
[例]
問 座標系
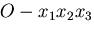 に対して,9つの成分を持つ量
に対して,9つの成分を持つ量
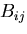 が,
が,
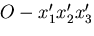 に対して,
に対して,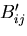 と,
と,
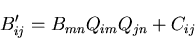 |
(81) |
で,関係づけられるとき,
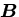 は,テンソルか?
は,テンソルか?
答 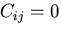 ならば,テンソルであるが,
ならば,テンソルであるが,
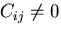 ならば,テン
ソルではない.
ならば,テン
ソルではない.
[例]
テンソルの成分が全て0であるとき,任意の変換に対して,変換後
もテンソルの成分は全て0である.
すなわち,
 |
(82) |
ならば,
 |
(83) |
である.
[例]
座標系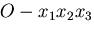 で,テンソルの成分に関する方程式が得られ
ているとする.
で,テンソルの成分に関する方程式が得られ
ているとする.
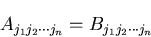 |
(84) |
これを書き換えて,
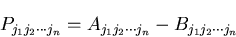 |
(85) |
と置くと,
 |
(86) |
ゆえに,
 |
(87) |
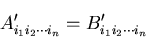 |
(88) |
結局,ある座標系で得られたテンソルの成分の方程式は,別の座標
系でも同じ形の方程式で表される.これをテンソルの座標不変性
(coordinate invariance)という.
Akihiro Nakatani
2001-06-25
![]() が,4個の指標を持つ81個の成分
が,4個の指標を持つ81個の成分![]() と,
と,
![]() で表されるとき,
で表されるとき,
![]() に対して,9つの成分を持つ量
に対して,9つの成分を持つ量
![]() が,
が,
![]() に対して,
に対して,![]() と,
と,
![]() ならば,テンソルであるが,
ならば,テンソルであるが,
![]() ならば,テン
ソルではない.
ならば,テン
ソルではない.
![]() で,テンソルの成分に関する方程式が得られ
ているとする.
で,テンソルの成分に関する方程式が得られ
ているとする.