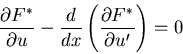区間![\([a,b]\)](img1353.gif) の低積分で次式のように表わせる
関数
の低積分で次式のように表わせる
関数 が変われば別の値になるような対応関係を考える.
が変われば別の値になるような対応関係を考える.
![\begin{displaymath}
I[u(x)]=\int_a^b F[u(x)] dx
\end{displaymath}](img1355.gif) |
(563) |
この"関数 実数"の対応関係を汎関数
(functional)という.
実数"の対応関係を汎関数
(functional)という.
汎関数は,「関数の関数」であり, はその変数に相当し,
変関数(variable function)と呼ばれる.
はその変数に相当し,
変関数(variable function)と呼ばれる.
数学や物理学における変分問題の例としては,
等周問題(周の長さが一定の曲線で囲まれた領域の面積を最大にする問題)
エネルギー原理,ハミルトンの原理など変分原理と称される問題がある.
ここで汎関数,
![\begin{displaymath}
I[u(x)]=\int_a^b F[x, u, u'] dx
\end{displaymath}](img1359.gif) |
(564) |
の停留値問題を考える.ここで,
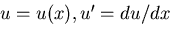 とおいている.
境界条件として,
とおいている.
境界条件として,
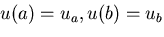 が規定されているとする.
が規定されているとする.
![\(I[u]\)](img1362.gif) を停留化する関数を
を停留化する関数を 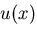 と書く.
任意の許容関数(admissible function,
上記の境界条件と必要な微分可能性の条件を満足する関数)
と書く.
任意の許容関数(admissible function,
上記の境界条件と必要な微分可能性の条件を満足する関数)
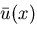 は次のように表わせる.
は次のように表わせる.
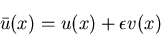 |
(565) |
ここで,
のような Taylor 展開を考え,これを
![\begin{displaymath}
I[u(x)+\epsilon v(x)]-I[u(x)]=\delta I + \delta^2 I + \cdots
\end{displaymath}](img1369.gif) |
(567) |
と表わす.
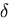 は変分作用素(変分演算子)であり,
は変分作用素(変分演算子)であり,
![\begin{displaymath}
\delta I = \left\{\lim_{\epsilon \rightarrow 0}
\frac{I[u(x)+\epsilon v(x)]-I[u(x)]}{\epsilon}\right\}\epsilon
\end{displaymath}](img1371.gif) |
(568) |
のように作用する.
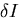 ,
, 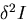 は,
は,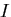 の第1変分
(first variation),
第2変分(second variation)
と呼ばれる量である.汎関数
の第1変分
(first variation),
第2変分(second variation)
と呼ばれる量である.汎関数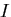 の停留条件は,
の停留条件は,
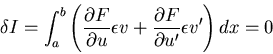 |
(569) |
によって与えられる.
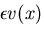 を
を 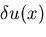 ,
,
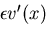 を
を 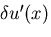 と書くと,
と書くと,
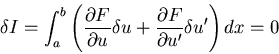 |
(570) |
部分積分すれば,
![\begin{displaymath}
\delta I= \left[\frac{\partial F}{\partial u'}\right]_a^b+
\...
...ft(\frac{\partial F}{\partial u'}\right)\right]\delta u dx = 0
\end{displaymath}](img1380.gif) |
(571) |
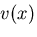 に関する条件から,第1項は零なので,
に関する条件から,第1項は零なので,
![\begin{displaymath}
\delta I= \int_a^b \left[\frac{\partial F}{\partial u}-
\fra...
...ft(\frac{\partial F}{\partial u'}\right)\right]\delta u dx = 0
\end{displaymath}](img1382.gif) |
(572) |
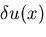 は任意に変化できるので,被積分関数が区間
は任意に変化できるので,被積分関数が区間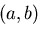 に
おいて零になる必要がある(変分学における基本補助定理
)ので,
に
おいて零になる必要がある(変分学における基本補助定理
)ので,
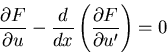 |
(573) |
となる.汎関数の停留問題に対する Euler方程式と呼ばれる.
この過程を要約すると,
となる.
次に,付帯条件,
![\begin{displaymath}
\int_a^b G[x, u, u']dx=0
\end{displaymath}](img1386.gif) |
(574) |
のもとでの汎関数![\(I[u(x)]\)](img1387.gif) の停留化を考える.
Lagrangeの未定乗数
の停留化を考える.
Lagrangeの未定乗数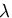 を導入して,
を導入して,
![\begin{displaymath}
H(u)=\int_a^b F[x, u, u'] dx + \lambda \int_a^b G[x, u, u']dx
\end{displaymath}](img1388.gif) |
(575) |
を定義すると,
となる.ここで,
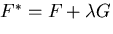 とおいている.
とおいている.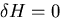 の条件から,
の条件から,
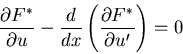 |
(577) |
と
![\begin{displaymath}
\int_a^b G[x, u, u']dx=0
\end{displaymath}](img1386.gif) |
(578) |
が得られる.
Akihiro Nakatani
2001-06-25
![]() の低積分で次式のように表わせる
関数
の低積分で次式のように表わせる
関数![]() が変われば別の値になるような対応関係を考える.
が変われば別の値になるような対応関係を考える.
![$\displaystyle \int_a^b F[x, u + \epsilon v, u' + \epsilon v']dx - \int_a^b F[x, u, u']dx$](img1366.gif)
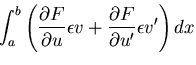
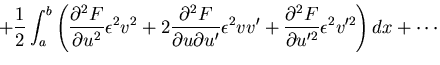
![\begin{displaymath}
\delta I = \left\{\lim_{\epsilon \rightarrow 0}
\frac{I[u(x)+\epsilon v(x)]-I[u(x)]}{\epsilon}\right\}\epsilon
\end{displaymath}](img1371.gif)
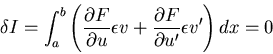
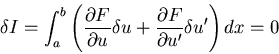
![\begin{displaymath}
\delta I= \left[\frac{\partial F}{\partial u'}\right]_a^b+
\...
...ft(\frac{\partial F}{\partial u'}\right)\right]\delta u dx = 0
\end{displaymath}](img1380.gif)
![\begin{displaymath}
\delta I= \int_a^b \left[\frac{\partial F}{\partial u}-
\fra...
...ft(\frac{\partial F}{\partial u'}\right)\right]\delta u dx = 0
\end{displaymath}](img1382.gif)
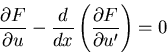
![$\displaystyle \int_a^b \delta F[x, u, u'] dx
+ \lambda \int_a^b \delta G[x, u, u'] dx
+ \delta\lambda \int_a^b G[x, u, u'] dx$](img1390.gif)
![$\displaystyle \left[\frac{\partial F^*}{\partial u'}\delta u\right]_a^b
+\int_a...
...{\partial u'}\right)\right]\delta u dx
+ \delta \lambda \int_a^b G[x, u, u'] dx$](img1391.gif)