Next: サンブナンの原理 Up: 重ね合わせの原理とサンブナンの原理 Previous: 重ね合わせの原理とサンブナンの原理 Contents Index
表面力
![]() と物体力
と物体力![]() が作用するもと
で生じる応力と変位をそれぞれ,
が作用するもと
で生じる応力と変位をそれぞれ,
![]() ,
,![]() とす
ると,
とす
ると,
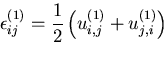 |
|||
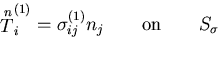 |
|||
| (493) |
これとは別に,表面力
![]() と物体力
と物体力![]() が作用するもとで生じる応力と変位をそれぞれ,
が作用するもとで生じる応力と変位をそれぞれ,
![]() ,
,
![]() とすと,
とすと,
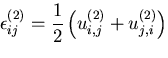 |
|||
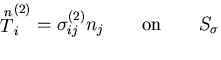 |
|||
| (494) |
これらの関係式はすべて線形の式であるから.それぞれの両辺を足しあわせた式,
![$\displaystyle [\epsilon^{(1)}_{ij}+\epsilon^{(2)}_{ij}]
=\frac{1}{2}\left[
\lef...
...}_{i}+u^{(2)}_{i}\right)_{,j}
+\left(u^{(1)}_{j}+u^{(2)}_{j}\right)_{,i}\right]$](img1192.gif) |
|||
![$\displaystyle [{\stackrel{n}{T}}^{(1)}_i+{\stackrel{n}{T}}^{(2)}_i]
=[\sigma^{(1)}_{ij}+\sigma^{(2)}_{ij}]n_j
\qquad {\rm on} \qquad S_\sigma$](img1194.gif) |
|||
| (495) |
重ね合わせの原理を用いると複雑な境界条件の問題を簡単な境界条件の和で表 すことができる.
Akihiro Nakatani 2001-06-25