図のような微小な四面体を考える.
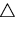 ABC の面積を
ABC の面積を 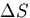 ,
その面の単位法線ベクトル
,
その面の単位法線ベクトル
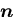 の成分を
の成分を
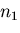 ,
,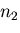 ,
,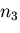 とする.
また,
とする.
また,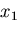 ,
,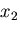 ,
,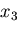 方向に垂直な面
方向に垂直な面
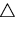 OBC ,
OBC ,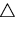 OCA ,
OCA ,
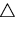 OAB の面積を
OAB の面積を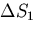 ,
,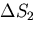 ,
,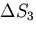 とすると,
とすると,
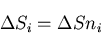 |
(125) |
となる.
ところで,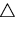 ABCの面にはたらく応力ベクトルは,
ABCの面にはたらく応力ベクトルは,
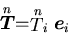 |
(126) |
となる.
一般に,物体には,上で述べた応力ベクトルのように
面を通して作用する力,すなわち,表面力
(surface force) のほかに,
重力,遠心力,電磁気力などのように,質量に比例してはたらく力,
物体力(body force)がある.
ここでは,物体が均質であるとして単位体積当たりの物体力を,
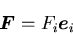 |
(127) |
とする.さて,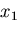 方向の力のつりあいを考えると,
方向の力のつりあいを考えると,
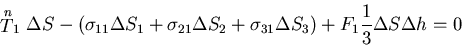 |
(128) |
となる.ここで,高次の項を省略して,
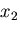 および
および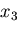 方向も同様に考えることによって
方向も同様に考えることによって
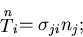 |
(129) |
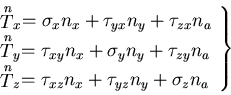 |
(130) |
を得る.
これをコーシーの関係
(Cauchy's relation),
または,コーシーの公式
(Cauchy's formula)という.
これにより,応力がテンソルであることがわかる.
以下では,商法則を用いて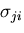 が2階のテンソルであることを
示す.
まず,
が2階のテンソルであることを
示す.
まず,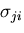 がテンソルか否かわからないので,とりあえず,
指標
がテンソルか否かわからないので,とりあえず,
指標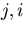 を有する,
を有する,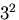 個の関数
個の関数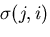 とする.
ベクトル
とする.
ベクトル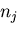 を掛けて(
を掛けて(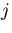 について和をとる)ことによって,
ベクトル
について和をとる)ことによって,
ベクトル
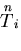 になることが分かっている.
さて,
になることが分かっている.
さて,
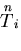 ,
,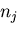 はベクトルであるから,
はベクトルであるから,
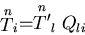 |
(131) |
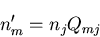 |
(132) |
のように変換される.ゆえに,
![\begin{displaymath}[\sigma(j,i)n_j]=\stackrel{\mbox{\scriptsize\(n\)}}T_i
=\stac...
...=
[{\sigma}'(m,l) n'_m]Q_{li}
={\sigma}'(m,l) Q_{mj}Q_{li} n_j
\end{displaymath}](img380.gif) |
(133) |
となる.そして,これが,任意の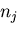 について成り立つためには,
について成り立つためには,
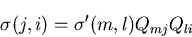 |
(134) |
が成立しなければ成らない,これは,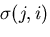 と
と
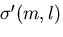 が2階のテンソルの変換法則を満足していることにほかならない.
このように,未知の量にテンソル(ベクトル)を乗じた結果がテンソル(ベクトル)
であることが分かっている場合に,その未知の量はテンソルである.
これを,テンソルの商法則
(quotient rule; quotient law)という.
つまり,
が2階のテンソルの変換法則を満足していることにほかならない.
このように,未知の量にテンソル(ベクトル)を乗じた結果がテンソル(ベクトル)
であることが分かっている場合に,その未知の量はテンソルである.
これを,テンソルの商法則
(quotient rule; quotient law)という.
つまり,
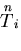 ,
,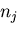 はともにベクトル
であり,
はともにベクトル
であり,
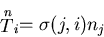 |
(135) |
なる関係が成り立っているから,
商法則によって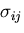 は2階のテンソルであることがわかる.
は2階のテンソルであることがわかる.
考えている量がテンソルであるかどうかは重要な事項である.
構成式は,同一の荷重に対する変形や,
同一の力学条件のもとで壊れたり,壊れなかったりといった違いが
座標のとり方に依存するのはおかしいから,テンソルの変換法則を
満足する量で記述されなければならない.
Akihiro Nakatani
2001-06-25
![]() ABC の面積を
ABC の面積を ![]() ,
その面の単位法線ベクトル
,
その面の単位法線ベクトル
![]() の成分を
の成分を
![]() ,
,![]() ,
,![]() とする.
また,
とする.
また,![]() ,
,![]() ,
,![]() 方向に垂直な面
方向に垂直な面
![]() OBC ,
OBC ,![]() OCA ,
OCA ,
![]() OAB の面積を
OAB の面積を![]() ,
,![]() ,
,![]() とすると,
とすると,
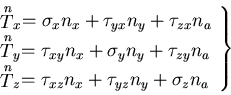
![]() が2階のテンソルであることを
示す.
まず,
が2階のテンソルであることを
示す.
まず,![]() がテンソルか否かわからないので,とりあえず,
指標
がテンソルか否かわからないので,とりあえず,
指標![]() を有する,
を有する,![]() 個の関数
個の関数![]() とする.
ベクトル
とする.
ベクトル![]() を掛けて(
を掛けて(![]() について和をとる)ことによって,
ベクトル
について和をとる)ことによって,
ベクトル
![]() になることが分かっている.
さて,
になることが分かっている.
さて,
![]() ,
,![]() はベクトルであるから,
はベクトルであるから,