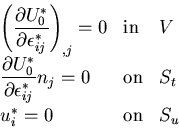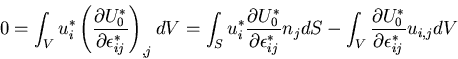微小変形理論においては,ある与えられた境界条件を満足する解は
ただ一つに存在することが証明される.
いま,与えられた境界条件を満足する2組の解が存在するとする.
このとき,変位,応力,ひずみが,それぞれ,
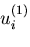 ,
,
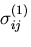 ,
,
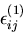 ,および,
,および,
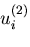 ,
,
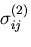 ,
,
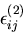 とする.
これらの2つの解はそれぞれ,つりあい方程式を満足するから,
とする.
これらの2つの解はそれぞれ,つりあい方程式を満足するから,
 |
(365) |
ここで,2つの解の差
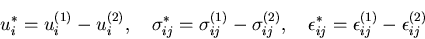 |
(366) |
を考えると,
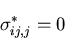 |
(367) |
となる.
一方,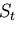 上での境界条件から,
上での境界条件から,
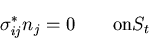 |
(368) |
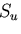 上での境界条件から,
上での境界条件から,
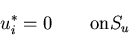 |
(369) |
すなわち,2つの解の差の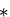 をつけた成分は,
弾性体の領域内で物体力の無いつりあい方程式を満足し,
境界上の力学的境界条件が
与えられるところで表面力が0,幾何学的境界条件が与えられるところで
変位が0となっている.
つまり,
をつけた成分は,
弾性体の領域内で物体力の無いつりあい方程式を満足し,
境界上の力学的境界条件が
与えられるところで表面力が0,幾何学的境界条件が与えられるところで
変位が0となっている.
つまり,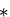 をつけた成分に関する
ひずみエネルギ密度関数
をつけた成分に関する
ひずみエネルギ密度関数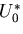 を用いて応力成分を書き直せば,
を用いて応力成分を書き直せば,
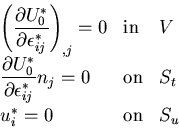 |
(370) |
となる.
この最初の式の両辺に 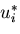 を掛けて領域にわたって積分すれば,
を掛けて領域にわたって積分すれば,
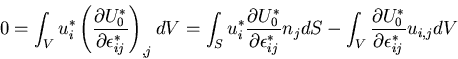 |
(371) |
第1項は,境界条件より0となる.また,
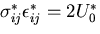 を用いると,
を用いると,
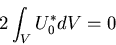 |
(372) |
さらに,ひずみエネルギは負にならないから,
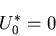 |
(373) |
を得る.さて,この式はひずみエネルギ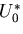 が零であることを意味している.
このためには,ひずみの成分が零であることを意味する.結局,
が零であることを意味している.
このためには,ひずみの成分が零であることを意味する.結局,
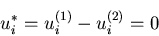 |
(374) |
となる.
したがって仮定した(1),(2)の解は同一となる.
このように,微小変形理論では解の唯一性が示される.
これを
キルヒホッフの解の唯一性の定理
(Kirchhoff's uniquness theorem)
という.
Akihiro Nakatani
2001-06-25
![]() ,
,
![]() ,
,
![]() ,および,
,および,
![]() ,
,
![]() ,
,
![]() とする.
これらの2つの解はそれぞれ,つりあい方程式を満足するから,
とする.
これらの2つの解はそれぞれ,つりあい方程式を満足するから,