Next: 最小コンプリメンタリエネルギの原理 Up: エネルギ原理 Previous: 最小ポテンシャルエネルギの原理 Contents Index
物体力と表面力を受けてつりあい状態にある物体の内部では, 応力はつりあい方程式と境界条件式を満足する.
このような実際に生じている応力を実応力といい,![]() とする.
これに対して,
とする.
これに対して,![]() 上の応力に関する境界条件,すなわち力学的境界条件は
満足するが,
上の応力に関する境界条件,すなわち力学的境界条件は
満足するが,![]() 上の変位に関する境界条件,すなわち,幾何学的
境界条件は必ずしも満足しないような仮想応力
(virtual stress)を
上の変位に関する境界条件,すなわち,幾何学的
境界条件は必ずしも満足しないような仮想応力
(virtual stress)を
![]() とあらわすことにする.
このような応力のことを静力学的に許容な応力
(statically admissible displacement)という.
とあらわすことにする.
このような応力のことを静力学的に許容な応力
(statically admissible displacement)という.
このような仮想応力が生じるためには,物体内部で,物体力が
![]() から,
から,
![]() に,
に,
![]() 上の表面力が
上の表面力が
![]() から,
から,
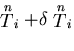 になることが考えられる.このとき,
になることが考えられる.このとき,
外部仮想仕事 ![]() に対応して,
に対応して,
| (344) |
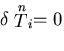 であることを考慮すると右辺第2項の面積積分の領域は,
であることを考慮すると右辺第2項の面積積分の領域は,| (345) |
| (346) |
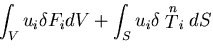 |
|||
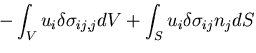 |
|||
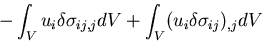 |
|||
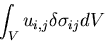 |
|||
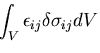 |
(347) |
これは,物体内部の力学的に許容な仮想応力
![]() が,幾何学的に許容なひずみ
が,幾何学的に許容なひずみ![]() に対してなす
内部コンプリメンタリ仮想仕事
(internal complementary virtual work)
に対してなす
内部コンプリメンタリ仮想仕事
(internal complementary virtual work)
![]() に対応することを意味している.
すなわち,
に対応することを意味している.
すなわち,
| (348) |
| (349) |
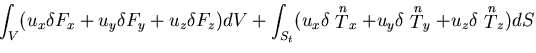 | |||
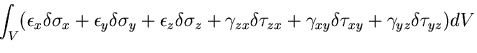 |
(350) | ||
この導出過程を逆にたどれば
コンプリメンタリ仮想仕事の原理は,ひずみ変位関係と
![]() 上の幾何学的境界条件と等価である.
ここで,導出の過程で
応力ひずみ関係などの構成式を導入していないので
すなわち,コンプリメンタリ仮想仕事の原理は,
応力ひずみ関係に無関係に成立しする.
上の幾何学的境界条件と等価である.
ここで,導出の過程で
応力ひずみ関係などの構成式を導入していないので
すなわち,コンプリメンタリ仮想仕事の原理は,
応力ひずみ関係に無関係に成立しする.
Akihiro Nakatani 2001-06-25