- 一般解を求めなさい.
-
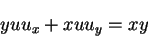 |
(1) |
略
-
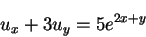 |
(2) |
(略解例)
特性曲線の方程式は,
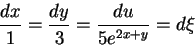 |
(3) |
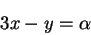 |
(4) |
すなわち,
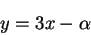 |
(5) |
一方,この関係を使うと,
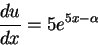 |
(6) |
積分すると,
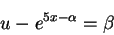 |
(7) |
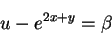 |
(8) |
よって,任意関数 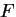 を用いて,陰関数として,
を用いて,陰関数として,
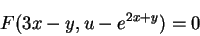 |
(9) |
あるいは,任意関数 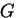 を用いて,陽関数として,
を用いて,陽関数として,
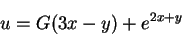 |
(10) |
-
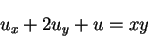 |
(11) |
(略解例)
特性曲線の方程式は,
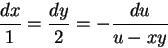 |
(12) |
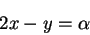 |
(13) |
一方,
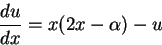 |
(14) |
両辺に,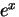 を掛けて,
を掛けて,
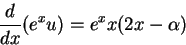 |
(15) |
積分すると(中略),
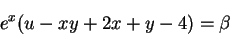 |
(16) |
よって,任意関数 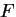 を用いて,陰関数として,
を用いて,陰関数として,
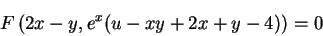 |
(17) |
あるいは,任意関数 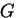 を用いて,陽関数として,
を用いて,陽関数として,
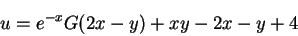 |
(18) |
Akihiro Nakatani
2001-09-25